Специальные функции
Формула для полиномов Эрмита имеет вид:

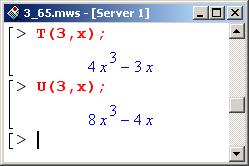
Ниже приведены примеры полиномов Чебышева.
Пожалуй, самое важное свойство описанных выше полиномов состоит в том, что они, как отмечалось, образуют ортогональные системы. Это свойство используется при разложении функций в ряд по ортогональным полиномам.
При выполнении таких разложений полезен пакет OrthogonalSeries, в котором предложен набор утилит, весьма полезных при работе с ортогональными разложениями.
Создать формальный ряд по ортогональным полиномам можно процедурой Create(). В качестве параметров процедуры указывают коэффициент разложения и тип полиномов, по которым выполняется разложение.
После подключения пакета OrthogonalSeries можно увидеть список процедур, которые стали доступными.

Среди этих процедур есть и Create(), которую используем для создания ряда.

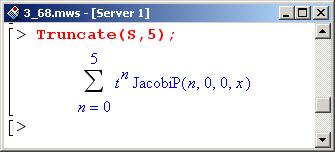
Оставим первые шесть слагаемых в ряде, для чего воспользуемся процедурой Truncate(). Первым параметром процедуры указывается ряд, вторым – индекс, на котором следует оборвать ряд.
Таким образом, получим следующее.