Специальные функции
Теперь заданную выше процедуру вызываем, указав первым параметром символ полинома Лежандра. Второй параметр определяет индекс полинома, третий – его аргумент. В результате получим следующее.

Однако при подстановке вместо конкретного значения для индекса полинома символьного значения (скажем, n) упростить приведенное выше выражение будет проблематично. Поэтому иногда удобно использовать представление для полиномов в виде суммы.
Задаем, согласно приведенной выше формуле, следующую зависимость.

На заметку
Результатом выполнения процедуры sum() в приведенной выше процедуре определения полиномов является выражение, которое требует упрощения. Если точнее, то в этом выражении следует сгруппировать слагаемые при соответствующих степенях аргумента, что и делается с помощью процедуры collect().
Таким образом, полином Лежандра можно вызвать теперь двумя способами: прописная литера Р соответствует определяемому системой полиному, строчная литера р – полиному, определенному пользователем. Например, альтернативой вызову Р(3,х) является следующее.
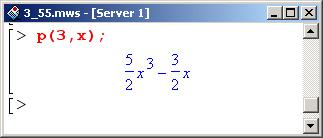
Как несложно заметить, результаты аналогичны. Проверим, что произойдет, если подставить определенные разными способами полиномы в уравнение, которому они по определению должны удовлетворять. Указав, что переменная m является целым неотрицательным числом (т.е. имеет тип nonnegint – указывается после двойного двоеточия в процедуре assume()), поочередно подставляем операторы генерирования полиномов Р() и р() в процедуру формирования уравнения (левой его части) ехргР().

Как видим, определяемые системой полиномы при таком вызове не упрощаются.
