Специальные функции
Еще одна важная проблема связана с почленным дифференцированием ряда. На этот случай в пакете Orthogonal Series имеется процедура Derivate(). Ниже будет показано, как дифференцировать ряд по ортогональным полиномам, но прежде создадим копию Rl ряда S, введенного ранее. Копия ряда создается с помощью процедуры Copy().

На заметку
Принципиальной разницы между использованием команд Rl: = S и Rl: = Copy(S) нет. Результаты выполнения обеих операций идентичны. Процедура Copy() введена разработчиками Maple в расчете на перспективу. Если в будущих версиях Maple пользователи получат возможность изменять внутренние таблицы данных Maple, использование команды присваивания в данном случае может привести к недоразумениям: изменения в ряде S будут автоматически применяться и к ряду R1. Пока такая проблема неактуальна, однако все же рекомендуется использовать процедуру Copy().
Теперь вычисляем производную.
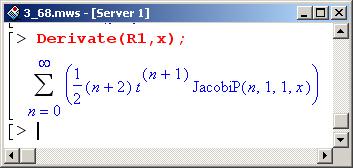
Иногда необходимо применить к ряду линейный дифференциальный оператор. В таких ситуациях полезна процедура ApplyOperator(). Рассмотрим пример ее использования. Для этого создадим новый ряд по полиномам Эрмита.

После этого к ряду R2 применяем оператор:

В полученном в результате выражении следует упростить коэффициенты разложения. Для этого вызываем процедуру SimplifyCoefficients(), указав первым параметром ряд, в котором следует упрощать коэффициенты, а вторым – процедуру упрощения (в данном случае это simplify).

