Интегральные преобразования
Задача 4.8
Необходимо функцию f(x) = ехр(-х) (x > 0) представить интегралом Фурье, продолжая ее а) четным и б) нечетным образом.
После подключения пакета описываем базовую преобразовываемую функцию.
При четном продолжении функции ее Фурье-образ будет совпадать (с точностью до множителя с косинус-преобразованием).
Соответственно, при нечетном продолжении используется синус-преобразование.
К полученным выражениям можно применить процедуру обратного преобразования invfourier().
Синтаксис ее вызова такой же, как и у процедуры прямого преобразования: сначала указывается преобразуемое выражение, затем переменная, относительно которой выполняется преобразование, и, наконец, переменная для функции.
Чтобы упростить эти выражения, сделаем предположение о положительности переменной х.
Выяснить, какова была исходная функция, можно следующим образом.
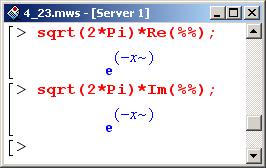
Здесь команда Re () вычисляет действительную часть аргумента, alm() – комплексную.
На заметку
Умножение выражения на комплексную единицу со знаком минус (-1) не эквивалентно вычислению комплексной части выражения. Это имеет место только в тех случаях, когда выражение чисто комплексное. Основанием для использования выше команд выделения действительной и мнимой частей явилось то, что косинус-образ является четной функцией, а синус-образ – нечетной. В силу этого, после обратного преобразования, в первом случае получаем действительное выражение, во втором – мнимое.
Кроме преобразования Фурье, достаточно часто используется преобразование Лапласа. Свойства образов функций в обеих случаях во многом схожи. Поэтому основанием для использования преобразования Лапласа, как правило, является невозможность выполнить преобразование Фурье.
На заметку
Дело в том, что преобразованию Фурье можно подвергнуть далеко не каждую функцию. Например, проинтегрировать f(x) = х при преобразовании Фурье не удастся. В отличие от преобразования Фурье, при преобразовании Лапласа ограничения на степень убывания преобразуемой функции в бесконечности не такие жесткие.
Преобразование Лапласа, наряду с преобразованием Фурье, является мощным инструментом исследования и, в частности, часто используется при решении дифференциальных уравнений.
В пакете Maple inttrans имеется процедура lарlасе() для выполнения преобразования Лапласа, а также процедура invlaplace() для выполнения обратного преобразования.
Синтаксис их вызова абсолютно такой же, как и у соответствующих процедур преобразования Фурье.