Тройные интегралы
Принципиальное отличие тройных интегралов от двойных состоит в том, что теперь появляется еще одна (третья) переменная интегрирования. Во всем остальном они схожи. Как и в случае двойных интегралов, основными методами вычисления тройных интегралов является сведение их к повторным и замена переменных в подынтегральных выражениях.
Все в том же пакете student для работы с тройными интегралами предусмотрена процедура Tripleint(), первыми четырьмя параметрами которой указываются интегрируемая функция и переменные интегрирования. Если диапазон изменения последних не указан, пятым параметром является область интегрирования (если точнее, то название этой области).
Для процедуры Tripleint() справедливы те же замечания, что и для процедуры Doubleint() – с той лишь поправкой, что переменных интегрирования три. Ниже показано, как эта процедура используется при решении задач.
Задача 4.14
Вычислить интеграл 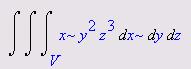 .
.

При этом главной проблемой является определение области интегрирования. В условии задачи заданы четыре уравнения, определяющие эту область. Три последних – уравнения плоскостей.
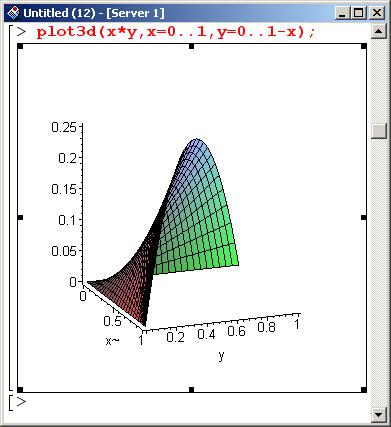
Ниже на графике показана поверхность, заданная уравнением z=xy.
На заметку
Трехмерные поверхности строятся с помощью процедуры plot 3d (). Для вызова этой процедуры никакой специальный пакет подключать не нужно. Параметры процедуры – уравнение поверхности и диапазон изменения переменных. Остальные параметры могут быть настроены с помощью кнопок контекстной панели, которая доступна при выделении рисунка в рабочем листе. Описание кнопок контекстной панели трехмерной графики можно найти в главе 1.