Криволинейные интегралы
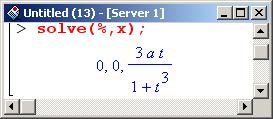
Теперь, когда параметрические зависимости заданы, можно вычислить интеграл.

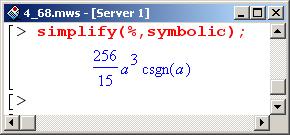
Последнее выражение следует упростить. При упрощении в процедуре simplify() после параметра – переменной среды %, ссылающейся на значение интеграла – указана опция symbolic.
В этом случае упрощение будет производиться в символьном виде. В частности, при вычислении квадратного корня из переменной в квадрате (в данном случае это переменная а) результатом будет сама эта переменная (а не ее модуль).
Криволинейные интегралы находят вполне конкретное практическое применение. В частности, с помощью криволинейных интегралов (второго рода) можно вычислять площади фигур, ограниченных кривыми.
Наиболее удобен такой подход, когда ограничивающие область кривые заданы в параметрическом виде.
Задача 4.18
С помощью криволинейного интеграла вычислить площадь фигуры, ограниченной кривой (Декартов лист).
Формально площадь фигуры, ограниченной кривой, может быть записана следующим образом.

Чтобы вычислить этот интеграл, необходимо параметризировать кривую, заданную следующим уравнением.

Предположим, что вдоль кривой координаты х, у и переменная-параметр t связаны следующим соотношением.
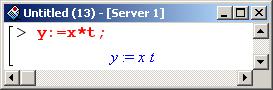
Подставляем это соотношение вместо у в уравнение кривой.

Полученное уравнение (в переменных х и t) решаем относительно х.