Поверхностные интегралы
Интеграл разобьем на две части: сначала вычислим интеграл по боковой поверхности конуса, а затем – интеграл по плоскости. Задаем уравнение боковой поверхности.

Кроме того, определяем подынтегральную функцию.

Эта функция в дальнейшем при вычислении интеграла будет умножаться на квадратный корень (с частными производными), который определим как функцию R двух переменных.

Можно проверить, чему эта функция равна для заданной ранее функции z.

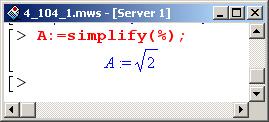
Это выражение упрощаем и присваиваем в качестве значения переменной А.
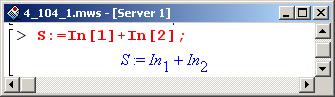
Как уже отмечалось, исходный интеграл (его значение запишем в переменную S) представляем в виде двух интегралов (это будут интегралы In[1] и In[2] – элементы массива In).
На заметку
Массив является множеством индексированных элементов. Во многом он напоминает список. Ссылка на элемент массива выполняется путем указания в квадратных скобках после названия массива индекса соответствующего элемента.
Теперь необходимо определиться с областью интегрирования в плоскости XY. Как нетрудно убедиться, для обеих поверхностей конуса (т.е. его боковой поверхности и основания) такой проекцией является круг радиуса 1; по этому кругу и следует интегрировать (в плоскости XY1). Интегрирование сначала выполняем по переменной х.
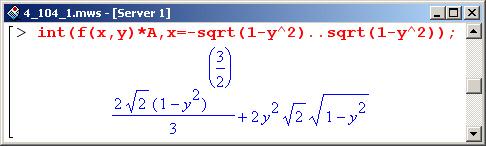
Полученное таким образом выражение интегрируем по у в пределах от -1 до 1.

Это значение присваиваем элементу In[1].

