Поверхностные интегралы
Поверхностные интегралы, как и криволинейные, делятся на интегралы первого и второго рода. В данном случае будут рассматриваться поверхностные интегралы первого рода, для которых поверхность, по которой выполняется интегрирование, задана в виде функции z(x,y).
Специальных процедур для вычисления поверхностных интегралов в Maple нет. Однако существующих утилит вполне достаточно для решения очень многих задач прикладного характера.
Задача 4.19
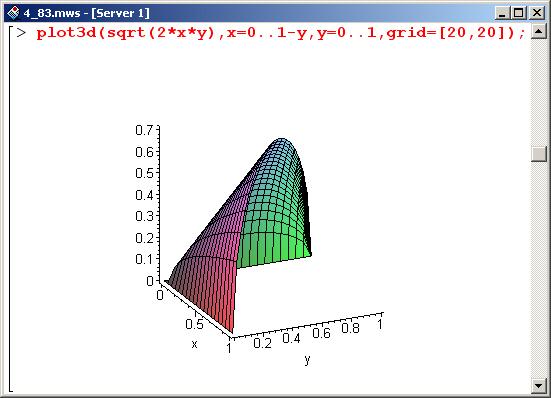
Найти площадь поверхности z =ху, отсекаемой плоскостями х + у = 1, х =0, у = 0, z = 0.
Для большего удобства определим процедуру, посредством которой поверхностный интеграл будет сводиться к повторному (и, разумеется, вычисляться). Данная процедура будет иметь четыре параметра: первый – интегрируемая функция (f); второй – это функция, задающая поверхность, вдоль которой вычисляется интеграл (z); и, наконец, два последних – переменные интегрирования с указанием диапазона их изменения.
Внимание!
Из сказанного выше следует, что если проекция поверхности интегрирования такова, что сразу указать диапазон изменения по каждой переменной не удается, – процедура для вычисления интеграла по такой поверхности неприменима. Другими словами, прежде чем использовать процедуру, следует определиться с областью интегрирования.

В процедуре локальным переменным t и и присваиваются в качестве значений левые части аргументов xRange и yRange. Эти параметры являются равенствами (например, х=а..b). Следовательно, левая часть такого равенства – это переменная, а правая часть – диапазон ее изменения.
В процедуре записан двойной интеграл, где подынтегральная функция умножается на соответствующий квадратный корень, содержащий частные производные от функции z, а в качестве диапазонов изменения переменных интегрирования указаны аргументы xRange и yRange.
Ниже представлена поверхность, по которой в данной задаче следует вычислить интеграл.