Тройные интегралы
Определяем границы интегрирования по каждой из переменных и записываем соответствующий тройной интеграл через повторный.
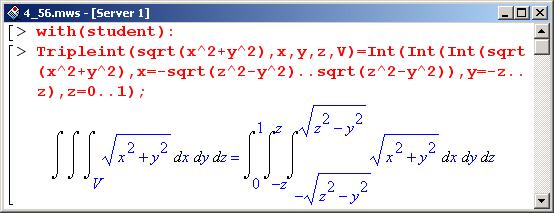
Нужно отметить, что особой трудности в вычислении записанного выше повторного интеграла нет. Однако вычислять его без замены переменных необходимо поэтапно. Проблема в том, что после интегрирования по очередной переменной придется производить упрощение и преобразование полученного выражения; иначе в силу громоздкости последнего Maple вычислить его не сможет.
В данном случае интеграл будет вычисляться посредством замены переменных, и с этой целью вызывается процедура changevar().
Синтаксис ее вызова такой же, как и при замене переменных в двойном интеграле, – указываются равенства, в соответствии с которыми вводятся новые переменные, выражение, в котором выполняется замена, и переменные, через которые следует записать интеграл.

Теперь осталось записать в новых переменных уравнения, определяющие границу области интегрирования. Для этого декартовые координаты выражаем через цилиндрические.

Внимание!
Стандартная процедура changecoords () после подключения пакета plots недоступна – будет вызвана одноименная процедура из указанного пакета.
В результате уравнение конуса будет записано следующим образом.

После упрощения получаем достаточно простое равенство.

Теперь можно вычислить интеграл.

Следует отметить, что в цилиндрических координатах переход к повторному интегралу от тройного осуществлялся безотносительно к повторному интегралу, записанному в исходных декартовых координатах. Этот интеграл рассматривался исключительно как иллюстрация методов перехода от многократных интегралов к повторным.
