Тройные интегралы
Область интегрирования получается, если эту поверхность рассечь тремя плоскостями:
- а) плоскостью, проходящей через ось z и прямую у=х в плоскости XY;
- б) плоскостью, параллельной осям z и у и пересекающей плоскость XY по прямой х=1;
- в) плоскостью XY.
Отсюда естественным образом определяем границы интегрирования по каждой из переменных и порядок интегрирования.

Однако, как и в случае двойных интегралов, зачастую сразу свести тройной интеграл к повторному не удается – приходится выполнять замену переменных.
Задача 4.15
Вычислить интеграл 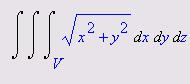 .
.
Первое, что сделаем после подключения пакетов (student – для использования процедур Tripleint() и changevar(), а plots – для вызова процедуры implicitplot3d()), – определимся с областью интегрирования.

Как несложно убедиться, область интегрирования является внутренней частью конуса, отсекаемой плоскостью y-1, параллельной плоскости XY.
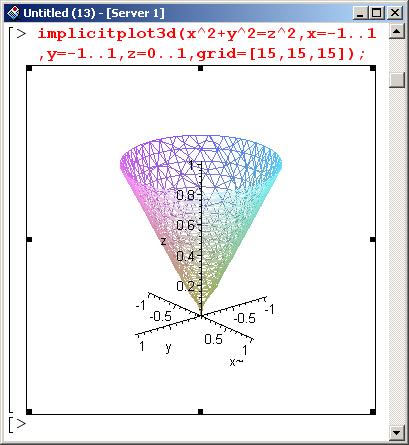
На заметку
Если пользователь в рабочем листе увидит рисунок, несколько отличающийся от приведенного выше, следует воспользоваться контекстной панелью трехмерной графики. Что касается процедуры implicitplot3d(), то она используется для отображения заданных в неявном виде поверхностей. Ее параметрами указывают уравнение, задающее поверхность, и диапазон изменения переменных. Опция grid задает число базовых точек, по которым строится поверхность (значение по умолчанию [10.10.10])
