Двойные интегралы
Теперь следует записать в новых переменных уравнения, определяющие область интегрирования. Переменной Omega присвоим в качестве значения определяющее область интегрирования неравенство (в декартовых координатах).
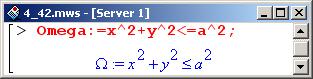
На заметку
Переменная Omega выглядит в области вывода как омега (Ω).
Переходим к полярным координатам.

Неравенство для области интегрирования выглядит теперь следующим образом.

На заметку
Кстати, замену переменных (т. е. выполнение перехода от декартовых координат к полярным в выражении для области) можно осуществить с помощью стандартной процедуры changecoords().
Таким образом, исходный двойной интеграл в полярной системе координат записывается через повторный следующим образом.
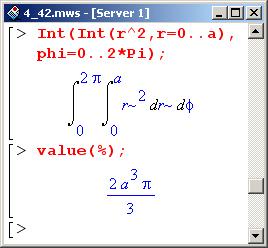
Видим, что и в достаточно простых случаях вычисление двойных интегралов требует от пользователя определенных усилий. Конечно же, Maple в полной мере избавить от рутинной работы не может, но все же его использование существенно ускоряет и упрощает процесс поиска решения.
