Решение обыкновенных дифференциальных уравнений
Чтобы задать функциональную зависимость x(t) согласно полученному выше равенству и не набирать его при этом непосредственно с клавиатуры, Воспользуемся процедурой unapply(). Эта процедура позволяет выделить функциональную зависимость, так что не придется прибегать даже к копированию выражения в буфер обмена.

Первым параметром процедуры unapply() указывается выражение, из которого "извлекается" функциональная зависимость, а вторым параметром – переменная, по отношению к которой определяется данная функциональная зависимость. Другими словами, результатом выполнения процедуры unapply() есть оператор, действие которого на указанную вторым параметром переменную продуцирует выражение, указанное первым параметром.
Оператор v определяем как результат действия оператора дифференцирования D на функциональный оператор х (в результате зависимость v(t) будет определять скорость парашютиста в момент времени t).
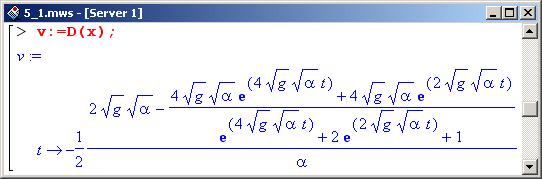
Скорость парашютиста в таком случае дается следующей закономерностью.

Полученное выражение можно упростить, причем существенно – с использованием гиперболических функций. Однако это задание оставляем читателю для самостоятельного решения.
Далее исследуем динамику парашютиста по прошествии существенных промежутков времени. Вычислительному ядру Maple сообщим, что параметры g и а положительны.

После этого вычисляем предел, к которому стремится скорость при стремлении времени к бесконечности.

Таким образом, в пределе бесконечно больших времен скорость парашютиста выходит на стационарное значение – движение будет равномерным.
Еще один интересный пример – математический маятник с трением. Об этом в следующей задаче.
