Решение обыкновенных дифференциальных уравнений
В результате выполнения приведенной ниже команды переменные получат значения.

Наличие в выражении экспонент смущать не должно: если параметр a меньше частоты в (это соответствует затухающим колебаниям), то показатели в экспонентах становятся комплексными и решения выражаются, на самом деле, через синус и косинус, правда с экспоненциальными множителями.
Чтобы представить, какова динамика системы во времени, присвоим конкретные значения константам. Если положить значение А равным 1, то для данных начальных условий х можно будет интерпретировать как значение координаты, нормированной на амплитуду колебаний.
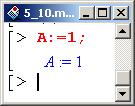
Положив Ω равной 1, переходим фактически к безразмерному времени (от t к mi). При этом параметр а можно интерпретировать как нормированный на частоту. Однако сделанные замечания носят скорее вспомогательный характер и сути проблемы не затрагивают.
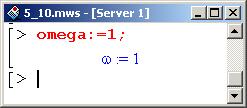
Далее строим график (если точнее, то поверхность) зависимости координаты маятника от времени и параметра а, определяющего трение в системе.
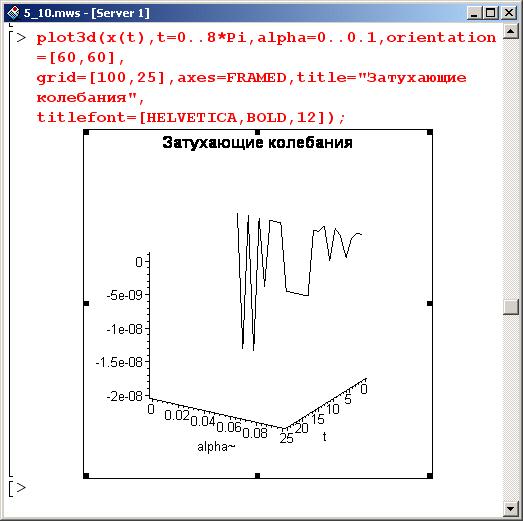
Несложно заметить, что с увеличением силы трения амплитуда колебаний затухает быстрее – что и не удивительно!
Приведенные выше примеры достаточно просты. Но Maple справляется и с более сложными задачами.
Некоторые из них приведены ниже.
