Приближенные методы решения дифференциальных уравнений. Метод разложения по малому параметру.
Преобразуем это уравнение, перенеся все слагаемые, содержащие малый параметр, в левую часть, а слагаемые, не содержащие малый параметр, – в правую. Сделать это можно с помощью процедуры isolate(). При вызове процедуры вычислительным ядром Maple предпринимается попытка в равенстве или алгебраическом выражении, указанном первым параметром, выразить подвыражение, указанное вторым параметром, т.е. фактически указанное первым параметром выражение решается относительно второго параметра-выражения.
Таким образом, получаем следующее.

Теперь можно собрать слагаемые при соответствующих степенях малого параметра (epsilon).

Неизвестные функции y0(x), y1(x) и у2(х) выбираются так, чтобы коэффициенты при степенях малого параметра (не всех, а только до второго включительно, до которого раскладывается в ряд искомая функция) равнялись нулю.
Отсюда получаем первое уравнение (для определения у0(х)), приравняв правую часть уравнения Eq (это коэффициент при нулевой степени параметра epsilon) к нулю.
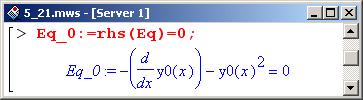
Приравнивая к нулю коэффициент при первой степени малого параметра, получаем еще одно уравнение.

В этом уравнении, помимо y1(x), присутствует и у0(х). Поэтому, прежде чем решать уравнение Eq_1, необходимо сначала решить уравнение Eq 0, найти тем самым у0(х), после чего можно будет решать Eq_1 относительно y1(x).
На заметку
Коэффициент при первой степени параметра epsilon определяется процедурой coef f (). Первым ее аргументом указана левая часть уравнения Eq (lhs(Eq)) – именно в левой части содержатся слагаемые с epsilon. Второй параметр (epsilon) является указанием на то, что нужно выделить коэффициент при первой степени epsilon. Приравняв этот коэффициент к нулю, получаем нужное уравнение.
Практически точно так же получаем последнее дифференциальное уравнение – приравниваем к нулю коэффициент при второй степени epsilon. Отличие от предыдущего случая состоит в том, что вторым параметром в процедуре coeff() указано epsilonA2.

