Приближенные методы решения дифференциальных уравнений. Метод разложения по малому параметру.
На следующем этапе выполняем разложение в ряд по малому параметру начальных условий. В данном случае начальное условие одно, и записано оно в переменную inCon. Эта переменная – равенство. Поэтому переносим все слагаемые в одну сторону – это делается командой (lhs(InCon)-rhs(InCon)) – и полученное выражение раскладывается в ряд по epsilon в окрестности нуля.

Теперь выражение трансформируется в полином.

В этом выражении присутствует функция у(0) (ее значение в точке 0), которая ищется в виде ряда. Поэтому следует выполнить соответствующую замену. Для этого введем переменную s, которой присвоим первоначальное значение у0(0).

Далее посредством оператора цикла к этой переменной будем прибавлять значения в данной точке функций-коэффициентов разложения, умноженных на малый параметр в соответствующей степени.
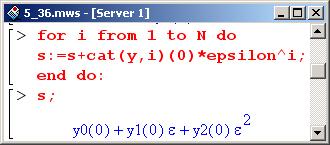
Теперь выполним замену.

Приравнивая коэффициенты приведенного выше полинома к нулю, получаем начальные условия для каждого из найденных ранее уравнений. Эти условия записываем в переменные inCon0, inCon1.

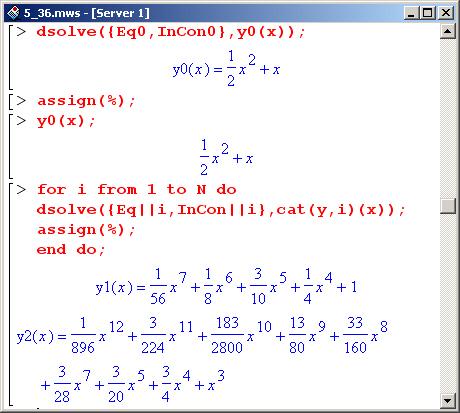
Решаем первое уравнение (приняв во внимание начальные условия).