Метод основанный на разложении искомой функции в ряд по аргументу
Еще один распространенный метод поиска приближенных решений дифференциальных уравнений основан на разложении искомой функции в ряд по аргументу в окрестности точки, в которой заданы начальные условия.
Задача 5.9
Найти решение в виде ряда для уравнения ху"(х)+у'(х)+ху(х) = чальными условиями у(0) = 1(0) = 0. с начальными условиями y(0)=1, y(0)=0.
Это уравнение имеет решение – функцию Бесселя j(x). Ниже попытаемся найти приближенное решение и сравнить его с точным.
Как обычно, задаем уравнение.
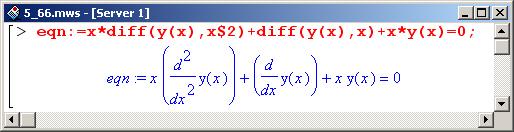
Начальные условия для этого уравнения имеют следующий вид.

Если решать данную задачу с помощью процедуры dsolve(), получим следующий результат.
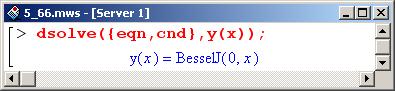
Чтобы получить приближенное решение в виде ряда, используем все ту же процедуру dsolve() практически с теми же параметрами; в конце добавлена опция series. Решение будет представлено рядом.

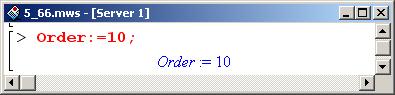
Количество слагаемых в ряде определяется значением переменной среды Order; значение этой переменной задает порядок остатка. Например, если нужно, чтобы последнее слагаемое было степени 9 по х, переменной Order присваиваем значение на единицу больше (т.е. 10).