Приближенные методы решения дифференциальных уравнений. Метод разложения по малому параметру.
Исходное уравнение при этом будет иметь такой вид.

Преобразуем это уравнение, перенеся все слагаемые в левую часть.
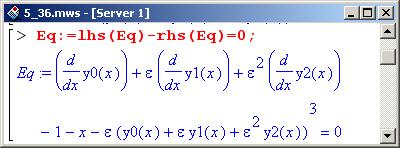
Далее левую часть уравнения Eq раскладываем в степенной ряд по параметру epsilon в окрестности нуля (команда series(lhs(Eq),epsilon=0,N+1)). Поскольку нас интересуют степени epsilon вплоть до N, в процедуре series () третьим параметром указано N+1 (на единицу больше) – этот параметр определяет порядок остатка, а сам ряд имеет порядок на единицу меньше.
Разложение преобразуем в полиномиальный вид (процедура convert()). Чтобы уравнение осталось уравнением, полученное выражение приравниваем к нулю.

Приравнивая коэффициенты разложения к нулю, получаем последовательность уравнений для определения приближенного решения.
Ниже такие уравнения формируются и присваиваются в качестве значений переменным.
Названия этих переменных являются объединением имени "Eq" и индекса i, который изменяется в диапазоне от 0 до N.

Коэффициент при i-й степени epsilon определяется процедурой coeff(). Степень epsilon указывается третьим параметром процедуры.
