Приближенные методы решения дифференциальных уравнений. Метод разложения по малому параметру.
Решать уравнения Eq_0, Eq_1 и Eq 2 следует строго в той последовательности, в какой они вводились. Причина очевидна – каждое последующее уравнение содержит, помимо неизвестной функции, еще и функции, которые определяются предыдущими уравнениями.
Переходим непосредственно к решению уравнений. Однако прежде сделаем некоторые замечания относительно начальных условий. В общем случае начальные условия также следует раскладывать в ряд по малому параметру. Коэффициенты разложения определяют начальные условия для уравнений, соответствующих тем же степеням параметра порядка. В данном случае малый параметр в начальных условиях не присутствует, поэтому начальным условием для уравнения нулевого порядка автоматически становится у0(х), а начальные условия для у1(х) и у2(х) – нулевые, поскольку отсутствуют (т.е. равны нулю) коэффициенты, начиная с первого порядка, разложения начальных условий в ряд по малому параметру.
Итак, получаем следующее.

Ниже, согласно полученному решению, выполняется присваивание.
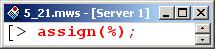
Внимание!
В этом месте функция у0(х) "технически" становится переменной!
Ситуация такая же, как и с функцией у(х). Например, если ввести команду у0(х), получим ожидаемый результат.
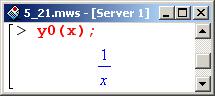
Однако если в приведенном выше вызове изменить аргумент (y0(t)), нужного значения (1/t) не получим.
Решаем теперь уравнение Eg 1 и находим y1(x).

В данном случае, перед присваиванием, раскладываем выражение для y1(x) на сумму дробей (процедура expand(%)).

Наконец, находим у2(х). Последовательность действий такая же.

