Задача о колебаниях струны конечной длины
Рассмотренный выше подход называется методом распространяющихся волн или методом Даламбера. Данный метод приемлем, в основном, при решении задач для бесконечных и полубесконечных областей. Ситуация несколько усложняется, если рассматривать струну конечной длины. Об этом следующая задача.
Задача 5.11
Требуется решить задачу о колебаниях конечной струны.
Уравнение не изменилось, однако здесь иная область, а также иные начальные и граничные условия. Нулевые граничные условия соответствуют ситуации, когда концы струны закреплены. Начальный профиль струны имеет вид выгнутой параболы.
Определим уравнение.
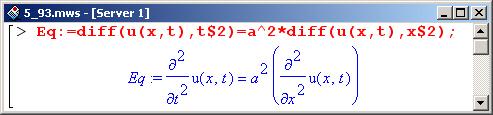
Решение будем искать методом разделения переменных. Этот метод подразумевает, что поиск решения осуществляется в виде произведения нескольких (в данном случае двух – по количеству переменных) функций, каждая из которых зависит от одного аргумента. В этом случае при вызове процедуры pdsolve() следует использовать опцию HINT, указав ее значение равным X(x)*T(t); именно в таком виде будем искать функцию u(x,t)=X(x)*T(t) (X(x) и T(t) являются неизвестными функциями одной переменной).
Таким образом, имеем следующее.

В полученном в результате выполнения команды выражении сначала указано, в каком виде искалась функция u(x,t), а затем в квадратных скобках после ключевого слова where (в переводе значит где) перечислены условия (уравнения), которым должны удовлетворять функции Х(х) и T(t).
Задаем уравнение для функции Х(х), заменив в нем для удобства переменную среды.
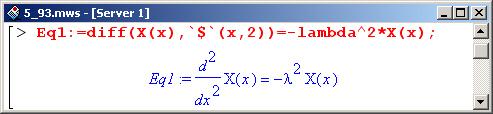
На заметку
Стоит обратить внимание на способ, которым с помощью оператора формирования последовательности ($) задана вторая производная. Здесь использована та особенность, что результатом выполнения команды '$' (х,2) является последовательность х,х.
Решаем это уравнение относительно Х(х), приняв во внимание одно из начальных условий, а именно: поскольку u(0,t)=X(0)T(t)=0, то Х(0)=0.
Получаем следующее.

