Задача о колебаниях струны конечной длины
Параметр λ должен быть таким, чтобы выполнялось и условие Х(1)=0. Но прежде чем решать соответствующее уравнение (относительно X), присвоим переменной среды _EnvAllSolutions, отвечающей за поиск всех решений уравнения, значение true.

В этом выражении переменная среды _Z1 "нумерует" собственные числа.
Внимание!
Выше, переменная среды _Z1 в области вывода содержит знак тильды. Это значит, что переменная может принимать далеко не любое значение; на нее наложены ограничения. Что это за ограничения, можно узнать, воспользовавшись процедурой about (). В данном случае в результате выполнения команды about(_Z1) появится сообщение "Originally renamed _Z1: is assumed to be: integer", что в переводе значит следующее: "В исходном варианте _Z1, переименовано; предполагается, что имеет целочисленный тип (integer)".
Поэтому можем задать зависимость, определяющую собственные числа краевой задачи (именно так называются найденные выше значения для lambda).

После этого определим собственные функции – такие функции, которые соответствуют собственным числам задачи.

Решение искалось такое, чтобы оно автоматически удовлетворяло одному из начальных условий (равенство нулю производной в начальный момент). Поскольку возможные значения для lambda определены выше (зависимость nu(n)), заменяем параметр lambda на nu(n) и определяем базовые функции, соответствующие собственным числам.
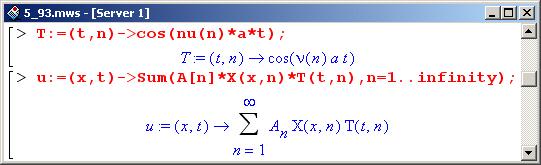
Неизвестные коэффициенты разложения А[n] находятся из начального условия. Согласно условию задачи, в начальный момент профиль струны определяется следующей функцией.

