Задача для полубесконечной струны
Практически так же решается задача и для полубесконечной струны – условие задачи такое же, но только в этом случае 0 < х < +∞. Кроме того, следует задать значение функции u(0,t) на левой границе. Если левый конец струны закреплен, то это значит, что u(0,t)=0.
Именно такую ситуацию и рассмотрим.
Для полубесконечной струны с нулевым граничным условием задача может быть решена, если рассмотреть бесконечную струну с начальными условиями, продленными на отрицательные значения аргумента нечетным образом.
Начальное отклонение возьмем в виде выгнутой вверх параболы.

Функцию f(x) получаем из функции f1(x) путем нечетного продолжения последней, т.е .f (x)=f1(x) при х>0 и f (x)=-f1(-x) – в противном случае.

Это решение отображаем в динамическом режиме.
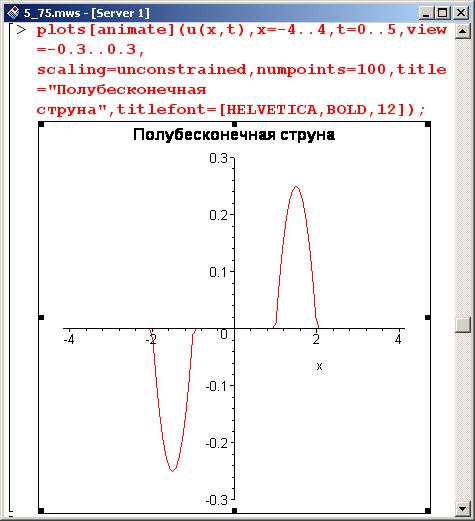
Полубесконечная струна в антисимметричном отображении. Первый (начальный) кадр: