Метод основанный на разложении искомой функции в ряд по аргументу
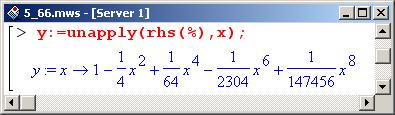
В этом случае приближенное решение будет следующим.

То, что последнее слагаемое имеет степень 8, объясняется просто: в разложении присутствуют только четные степени х, т.е. коэффициенты при нечетных степенях – нули.
Полученное приближенное решение сравним с точным. Для этого преобразуем приближенное решение в полиномиальный вид.

Результат преобразования возьмем за основу, для того чтобы задать соответствующую функцию.
Ниже показаны кривые для точного и приближенного решений.
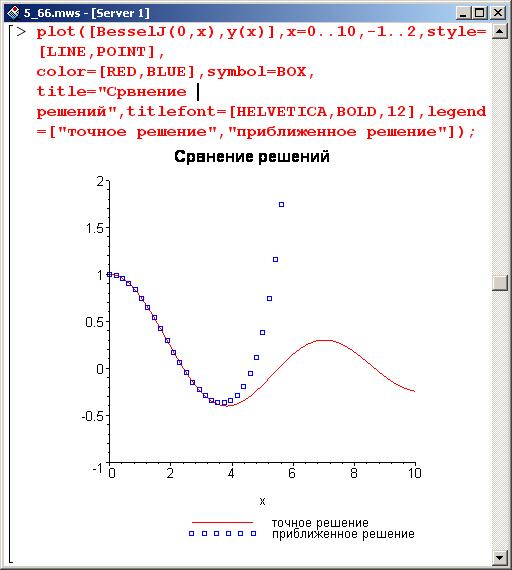
Видим, что в окрестности точки 0, где задавались начальные условия, вполне приемлемо использовать приближенное решение.
