Приближенные методы решения дифференциальных уравнений. Метод разложения по малому параметру.
Описываем процедуру spDiffSol(), которая будет иметь пять параметров: решаемое дифференциальное уравнение Eq, начальные условия InCon, функция fnc (с указанием аргумента!), относительно которой решается уравнение, малый параметр epsilon и целое неотрицательное число n, определяющее порядок разложения по малому параметру при нахождении решения.
После каждого из перечисленных параметров стоит двойное двоеточие (::), после которого указывается тип параметра. Так, equation (этот тип имеют первый и второй параметры) определяет уравнение. Третий параметр имеет тип функция (function). Малый параметр имеет символьный тип (symbol) и, наконец, последний, пятый, параметр – целое неотрицательное число (тип nonnegint).
Если в дальнейшем при вызове процедуры хотя бы один из ее параметров будет иметь иной тип, появится сообщение об ошибке. Если напрямую тип не указывать, будет предпринята попытка выполнить процедуру и, скорее всего, ошибка возникнет непосредственно в процессе выполнения – такие ошибки отслеживать сложнее.
Внимание!
Как сказано выше, второй параметр, определяющий начальные условия, имеет тип равенство. Это справедливо только в том случае, если такое условие одно. Известно, что [для однозначного решения дифференциального уравнения число начальных условий должно равняться порядку этого уравнения. Таким образом, процедура может использоваться для решения задачи Коши только для уравнений первого порядка. Из сказанного, Однако, не следует, что с помощью создаваемой процедуры нельзя будет решать уравнения более высоких порядков. Просто в этих случаях такие решения придется искать в 1 общем виде, а присутствующие в решениях произвольные константы потом самостоятельно находить из начальных условий.
Назначение локальных переменных будем рассматривать по мере их использования.
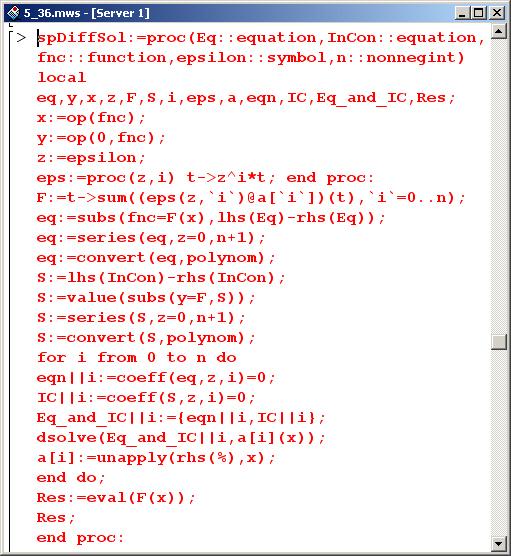
Первой определяется переменная х, которой в качестве значения присваивается операнд указанной аргументом функции fnc (op(fnc)), т.е. ее аргумент. Переменной у присваивается нулевой операнд функции fnc (команда op(0,fnc)); для функциональных зависимостей таким операндом является имя функции. Эти переменные, следовательно, определены так, чтобы тождественно выполнялось равенство y(x)=fnc. Кроме того, для удобства малый параметр запишем в переменную.
На следующем этапе в теле процедуры определяется другая процедура eps() – локальная, т.е. вне процедуры spDiffSol данная процедура будет недоступна! – при действии которой на аргумент t (т.е. процедурой определяется оператор) этот аргумент умножается на первый параметр процедуры г, возведенный в степень, определяемую вторым параметром процедуры i.
