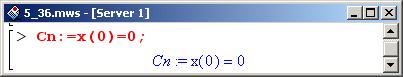Приближенные методы решения дифференциальных уравнений. Метод разложения по малому параметру.
Далее следует процедура dsolve(), с помощью которой уравнение eqn| |i с граничным условием IC||i (они являются элементами множества Eq_and_IC||i) решается относительно функции a[i](x). Поскольку результат решения представляется в виде равенства, после нахождения решения следует, согласно равенству-решению, определить функцию a[i](x) (если точнее, то оператор a[i]). Результат действия оператора a[i] на аргумент х определяется правой частью равенства, полученного в результате решения уравнения. Ссылка на этот результат выполнена посредством переменной среды %, а правая часть равенства, соответственно, возвращается командой rhs(%). Чтобы из этого выражения выделить оператор, используем процедуру unapply().
На этом команды оператора цикла заканчиваются.
По завершении описанного выше оператора цикла все уравнения решены, и в переменную Res записывается результат вычисления F(x).
Внимание!
Если не использовать процедуру eval(), а просто указать Res: = F(x), то результат выполнения процедуры будет представляться через коэффициенты a[i], без непосредственного вычисления результата их действия на аргумент х.
Последней командой процедуры является Res, в результате выполнения которой на экран выводится приближенное решение уравнения.
После того как определена процедура, логично проверить ее на предыдущей задаче, решение которой уже известно. Для "чистоты эксперимента" заново определим уравнение и начальные условия, заменив неизвестную функцию на f, аргумент – на t, а малый параметр – на mu (в области ввода – это mu, а в области вывода – μ). Ниже приведены соответствующие команды.
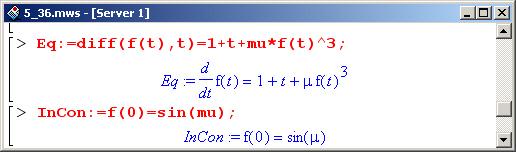
Ранее отмечалось, что с помощью созданной выше процедуры задачу Коши можно решать для уравнений первого порядка. Но процедура может использоваться и для решения уравнений более высоких порядков.
Например, запишем уравнение для ангармонических колебаний.

Это уравнение второго порядка, а малый параметр epsilon при квадратичном по отклонению слагаемом определяет степень ангармонизма (если параметр epsilon равен нулю, определяемые уравнением Eq2 колебания называются гармоническими).
Так как мы имеем уравнение второго порядка, для нахождения однозначного решения следует задать два начальных условия. Сначала запишем начальное условие для отклонения.