Уравнения в частных производных. Задача о колебаниях бесконечной струны.
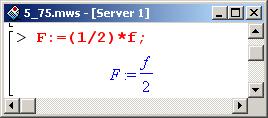
Константу можно положить равной нулю (несложно доказать, что общности метода это не ограничит), а функцию _F1 обозначим как F.
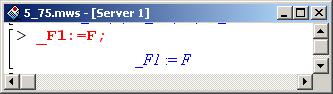
Тогда естественно определить функцию F2 следующим образом.

Следовательно, искать решение уравнения нужно в таком виде.
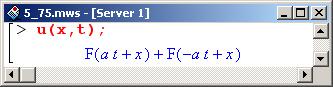
В последнем выражении присутствует уже только одна неизвестная функция F. При этом первое слагаемое F(at+x) описывает волну, распространяющуюся влево, а слагаемое F(-at+x) – волну, которая распространяется вправо. Непосредственно функцию F будем искать из оставшегося неиспользованным начального условия для значения функции u(x,t) в начальный момент времени.
Согласно полученному выражению для функции u(x,t), в начальный момент (при t=0) она равна следующему.
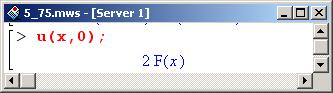
С другой стороны, это функция f (х), т.е. начальное отклонение струны. Для определенности возьмем функцию f (x) в таком виде.

Первоначальный профиль струны, таким образом, имеет форму симметричного треугольника.
На заметку
Функция Heaviside(x) равна 1 при х>0 и 0 – в противном случае.
Функция F тогда равна следующему.