Решение обыкновенных дифференциальных уравнений
Задача 5.2
Составить и решить дифференциальное уравнение для математического маятника с трением.
В отличие от уравнения для маятника без трения, в данном случае будет присутствовать слагаемое, пропорциональное скорости маятника, т.е. первой: производной. Для удобства коэффициент пропорциональности обозначим через a.
Таким образом, рассматриваем следующее уравнение.

Данное уравнение можно решить в общем виде; в этом случае начальные, условия не указываются.
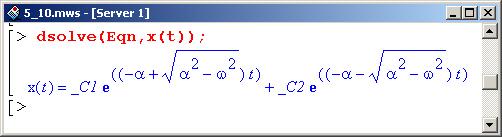
Переменные среды _С1 и _С2 являются, с математической точки зрения, произвольными константами, которые в общем случае определяются из дополнительных условий – как правило, начальных.
Далее с помощью уже известной процедуры unapply() определяем соответствующую функциональную зависимость.

Если предположить, что в начальный момент отклонение маятника от положения равновесия равнялось А, а начальная скорость была равна нулю, то константы С1 и С2 можно определить как решение системы уравнений (обычных, не дифференциальных!).
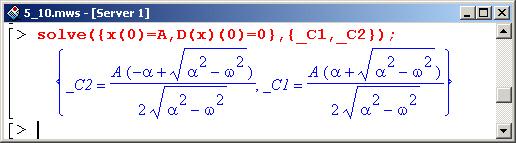
Чтобы переменным _С1 и _С2 присвоить соответствующие значения (при решении такие значения находятся, но не присваиваются), можно воспользоваться процедурой assign(). Если в качестве аргумента этой процедуры указано равенство, то, согласно этому равенству, вычислительным ядром Maple будет выполнено присваивание (формально можно полагать, что знак равенства заменяется оператором присваивания).
Ниже в качестве аргумента указана переменная среды – ссылка на результат выполнения последней команды. Это множество, элементами которого являются два равенства, определяющие переменные _С1 и _С2.
