Интерполяция методом Лагранжа
Параметрами процедуры plotl() определим список базовых интерполяционных точек и переменную интерполирования. Код процедуры приведен ниже.
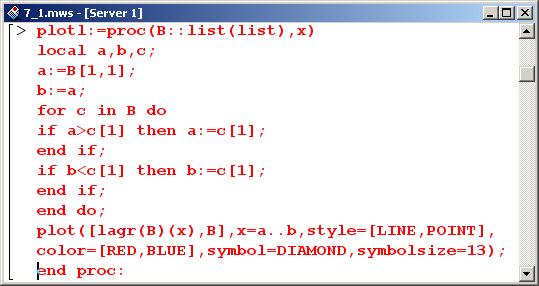
Локальные переменные а и b в теле процедуры используются для определения нижней и верхней границ области интерполирования соответственно Значения обеих переменных инициализируются равными первой указанной в списке-параметре процедуры интерполяционной точке (ссылка В [1.1]– первый элемент из первой пары "точка-значение" списка В). После этого перебираются все интерполяционные точки (ссылка с[1]), и если среди них встречается значение, меньшее текущего значения а, – оно присваивается этой переменной. Значение переменной b переопределяется в том случае, если выбранная точка имеет значение, большее текущего значения b.
В результате выполнения цикла в переменной а будет записана самая левая точка, в переменной b – правая. Наконец, вызывается процедура отображения двухмерной графики plot(), в которой отображаемыми функциями указаны интерполяционный полином Лагранжа, построенный по точкам списка В, а также сами эти точки. Ниже приведен пример вызова разработанной только что процедуры.
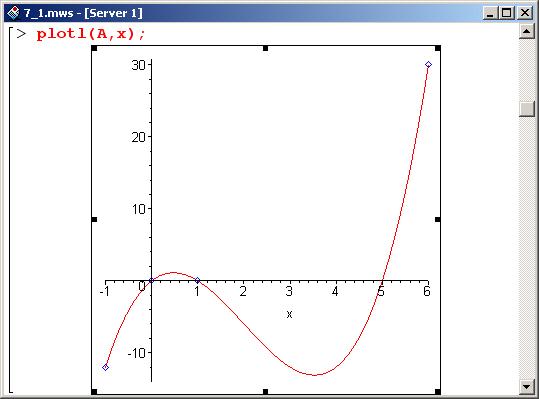
Аппроксимация зависимостей интерполяционными полиномами Лагранжа наиболее эффективна, когда интерполируемая функция сама является полиномом. В этом случае, если взять достаточное количество базовых точек, можно добиться абсолютного совпадения. Однако подобные ситуации случаются не часто, и вопрос о погрешности, возникающей вследствие интерполяции, представляется актуальным. Что касается непосредственно метода Лагранжа, то на границах области интерполирования соответствующие полиномы могут в значительной степени отклоняться от прямой, соединяющей соседние точки. Последнее далеко не всегда приемлемо.
