Общая задача интерполирования
В качестве базовых интерполяционных функций можно выбрать, по большому счету, любой их набор – главное, чтобы такие функции были независимы. Причем линейной независимости функций в обычном понимании этого термина в данном случае недостаточно. Предположим, что интерполяция выполняется по узлам х0,х1,…,хn. Количество базовых интерполяционных функций должно совпадать с количеством узловых точек. Пусть это будут функции. Чтобы функции могли использоваться в процессе интерполяции, они должны быть такими, чтобы любая их линейная комбинация имела на интервале интерполяции число корней (т.е. точек, где эта линейная комбинация обращаются в нуль) по крайней мере на единицу меньше, чем число базовых узлов. Такие системы функций еще называют системами Чебышева.
Интерполяционную функцию ищем в виде Fn(x) = a0<po(x) + a,<pt(x) +… + a,<pn(x). Коэффициенты а, находятся из тех условий, что в узловых точках значения интерполяционной функции совпадают с табулированными значениями интерполируемой функции: Fll(xl) = yi. Таким образом, имеем систему n+1 уравнений относительно n+1 неизвестного коэффициента а,. Из этих уравнений коэффициенты определяются однозначно.
Ниже представлен код процедуры, с помощью которой можно выполнять интерполяцию разными базовыми функциями.
Параметрами процедуры Mylnt() являются список базовых точек А, по которым строится интерполяционная функция, а также оператор f (), который задает общий вид базовых интерполяционных функций.
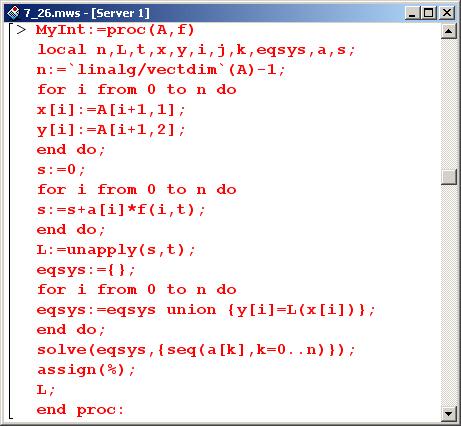
Исключительно в целях наглядности в самом начале процедуры задается два массива – узловых точек х и значений функции в этих точках у. Массивы определяются исходя из данных списка А. Переменная п инициализируется со значением, на единицу меньшим числа элементов списка А. В этом случае нумерация узлов начинается с индекса 0. Далее с помощью оператора цикла переменной s присваивается значение, структура которого совпадает со структурой искомой интерполяционной функции. В этом выражении коэффициенты a[i] являются неизвестными переменными, которые следует определить.
Используя выражение s в качестве основы, переменная L определяется как оператор, действие которого на аргумент t эквивалентно вычислению данного выражения.
На следующем этапе в процедуре определяется система уравнений eqsys, из которой будут искаться неизвестные коэффициенты разложения. Система поочередно дополняется уравнениями, которые фиксируют равенство значений интерполяционной функции L() заданным массивом у табличным значениям интерполируемой функции в узловых точках. Система решается относительно коэффициентов а[к], и полученные в качестве решения значения присваиваются этим коэффициентам (команда assign(%)). Результатом процедуры возвращается оператор L().
