Общая задача интерполирования
Теперь строим интерполяционную функцию.
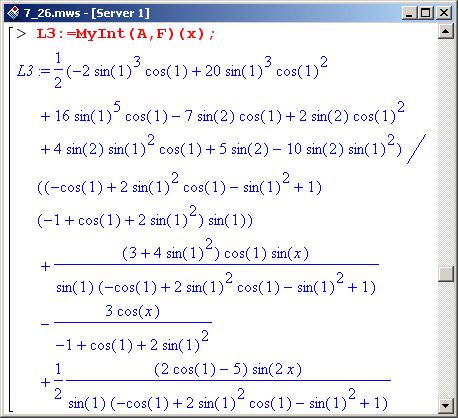
Полученное в результате выражение достаточно громоздко, поэтому преобразуем его, перейдя к формату представления чисел с плавающей точкой.
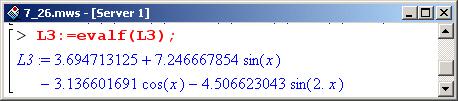
Помня о том, что нет такой формулы, которая была бы нагляднее картинки, построим две интерполяционные функции – по полиномам (L1) и тригонометрическим функциям (L3).
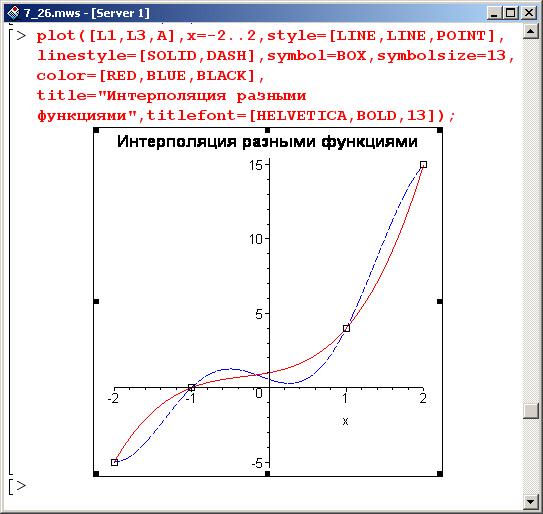
Сплошная линия для полиномиальной интерполяции, штрихованная – для интерполяции тригонометрическими функциями.
Видим, что функции ведут себя практически одинаково. Однако между такими интерполяционными функциями есть существенная разница, о которой следует помнить: при интерполяции степенными функциями, если выйти за пределы области интерполирования (в этом случае имеем дело с задачей экстраполяции), полином, в конечном счете, стремится к бесконечности, тогда как при интерполяции тригонометрическими функциями получаем ограниченную, периодичную интерполяционную функцию.
