Общая задача интерполирования
Проверим, как работает процедура. Для этого зададим следующий список.

В переменную L1 запишем интерполяционную функцию (полином), построенную по степенным функциям.
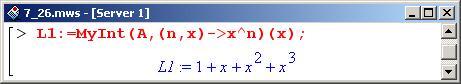
В качестве базовых интерполяционных функций можно взять ортогональные полиномы. Например, рассмотрим полиномы Чебышева первого рода, которые, как известно, задаются следующим образом.

Результат интерполирования по этим полиномам запишем в переменную L2.
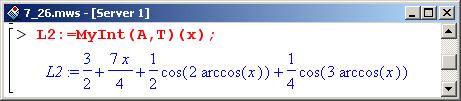
На первый взгляд кажется, что получено новое, отличное от L1, выражение, но это не так. Убедиться в последнем можно, упростив его.

Ничего удивительного в этом нет, ведь полиномы – есть полиномы, даже если это полиномы Чебышева.
Еще один класс функций, представляющих особый интерес, – тригонометрические функции.
Рассмотрим следующую систему.

На заметку
Командой iquo(n,m) в качестве результата возвращается целая часть от деления n на m, в то время как irem(n,m) есть остаток от целочисленного деления n на m.
Чтобы представить себе, что же за система функций задается оператором F(), рассмотрим такую последовательность.

Видим, что это набор тригонометрических функций (чередующиеся синусы и косинусы), используемых, корме прочего, при выполнении разложений в ряд Фурье.
Внимание!
Приведенная выше система функций часто используется для интерполирования периодических функций. Перечисленные функции в совокупности периодичны с периодом 2π. Поскольку в данном случае функция интерполируется на сегменте от -2 до 2, т.е. длина сегмента равна 4 (что меньше указанного периода), интерполяция возможна. В противном случае пришлось бы выполнять замену переменных.
