Интерполяция методом Ньютона
При интерполяции по методу Ньютона в результате получают тот же полином, что и при интерполяции Лагранжа. Причина проста и состоит в том, что в обоих случаях строят полином минимально необходимой степени, проходящий через заданные точки. Такой полином определяется однозначно и потому не зависит от способа, которым он получен. В этом смысле интерес представляет не получаемый результат, а скорее сам процесс его получения.
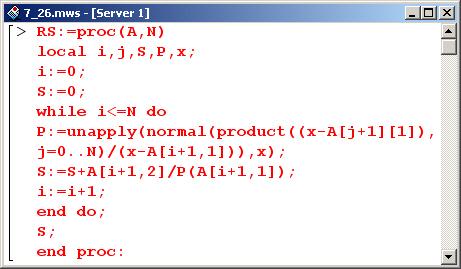
Параметрами процедуры RS() являются список А узловых точек и значений интерполируемой функции в этих точках, а также порядок N разделительной разности.
В начале процедуры инициализируются с нулевыми значениями переменные i и S. Далее следует условный оператор while. Проверяемым в этом операторе условием является неравенство i=N. Таким образом, команды из оператора цикла будут выполняться до тех пор, пока значение переменной i не превысит N. Изменение значения индексной переменной на единицу осуществляется последней командой в операторе цикла.
На заметку
Предложенный выше способ определения разделительных разностей основан на определении специальной функции Р() для вычисления произведения аргументов. В общем случае число таких функций на единицу больше порядка разделительной разности. Произведение можно было бы вычислить и без вызова функционального оператора более простым способом. Поэтому приведенный программный код носит скорее иллюстративный характер и призван показать возможности и преимущества командного языка Maple.
Теперь определим оператор, с помощью которого будем строить интерполяционный полином Ньютона.
Внимание!
Здесь еще раз хочется напомнить, что при интерполяции функции полиномом последний не зависит от способа его получения. В этом смысле, что полином Ньютона, что Лагранжа – все едино. Полином один и тот же. Название характеризует только способ, которым этот полином был получен.
Процедура newton() имеет только один параметр, который представляет собой список с узловыми точками и значениями функции.
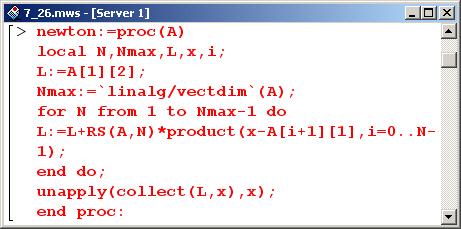
Локальная переменная L инициализируется со значением А[1][2]. Это значение интерполируемой функции в первой узловой точке. Далее переменной Nmax присваиваем в качестве значения длину списка А. С помощью оператора цикла, согласно формуле для интерполяционного полинома, формируем соответствующее выражение. В этом операторе, кроме прочего, вызывается и разработанная выше процедура определения разделительных разностей RS().
