Интерполяция методом Лагранжа
Как видно из рисунка, интерполяционные полиномы весьма далеки от совершенства. Полином по первому множеству вообще представляет собой прямую. Поэтому естественным образом возникает вопрос о том, как следует выбирать интерполяционные точки, чтобы полином наиболее адекватно описывал интерполируемую функцию. Понятно, что если исходная функция неизвестна и узловые точки заданы apriori, постановка такой задачи не имеет смысла. Однако, как уже отмечалось, часто нужно интерполировать известную функцию. В этом случае задача выбора узловых точек на интервале интерполирования полностью ложится на пользователя.
Не вдаваясь в детальный теоретический анализ, сформулируем сразу ответ (читателей, интересующихся данной проблемой, отсылаем к специальной литературе). Состоит он в том, что нам понадобится вычислить нули ортогональных полиномов Чебышева. Зачем это делается, будет объясняться по ходу изложения материала.
В главе 3 об ортогональных полиномах Чебышева первого рода речь уже велась. Можно, разумеется, использовать встроенную команду для вызова соответствующего полинома. Однако поскольку способ их определения достаточно прост, зададим собственную функцию, зависящую от двух аргументов: индекса полинома и непосредственно полиномиальной переменной.

Прежде чем искать нули полиномов, изменим значение переменной среды _EnvAllSolutions. Это нужно для того, чтобы при решении соответствующего уравнения искались все решения.

Теперь находим нули полинома Чебышева первого рода индекса n.

Решение представлено через переменную среды _Z1, которая в области вывода сопровождается тильдой. Это значит, что на переменную наложены ограничения. Чтобы узнать, каким условиям эта переменная должна удовлетворять, воспользуемся процедурой about().
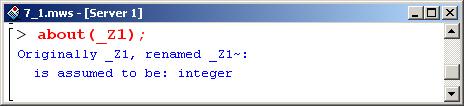
Перевод содержимого области вывода гласит, что исходная переменная _Z1 переименована в Z1∼ и предполагается, что это целое число.
Теория говорит о том, что для построения оптимального полинома, который при прочих неизменных условиях будет аппроксимировать функцию на интервале от -1 до 1 с наименьшей погрешностью (наименьшая верхняя граница для погрешности), в качестве базовых узлов следует взять нули полинома Чебышева порядка, который равен числу узловых точек. Другими словами, если базовый полином строится по 10 точкам, то и полином следует брать с индексом 10. Если интерполяция выполняется на интервале (а,b), отличном от интервала (-1.1), то узловые точки все равно выражаются через нули указанного полинома согласно формуле хπ =((b-а)со&{(2π+1)n/2n)+(b + а))/2.
