Интерполяция методом Лагранжа
Если третьим параметром указать число, погрешность также будет представлена числом. Посмотрим, что произойдет, если в качестве второго параметра указать узловую точку.

Ничего удивительного в том, что погрешность равна нулю, нет. Ведь в узловой точке, по определению, значение интерполяционного полинома точно совпадает со значением функции.
Нетрудно понять, что погрешность интерполирования зависит не только от интерполируемой функции, но и от выбора интерполяционных точек. Проиллюстрировать это можно следующим примером. Определим тригонометрическую функцию.
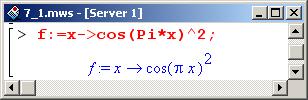
После этого создаем два списка. В каждом из этих списков табулируем значения функции по пяти узловым точкам. Однако узловые точки в каждом случае выбраны по-разному.
В первом случае выбираем равноудаленные узлы.
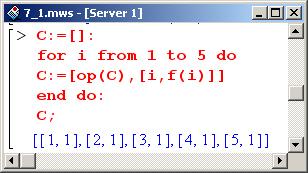
Во втором случае узлы выбираются согласно формуле xi=(i-1/i), а индексная переменная i пробегает значения от 1 до 5.
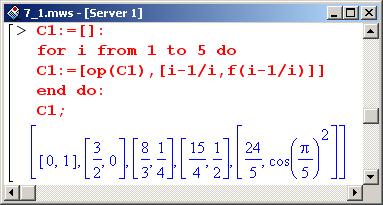
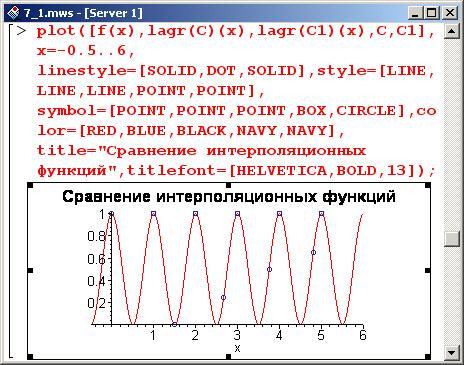
Теперь на одном рисунке отобразим все три графика: для интерполируемой функции и двух интерполяционных полиномов для каждого набора точек. Точки из первого набора, определяемого списком С, обозначены квадратами, а из второго набора, определяемого списком С1, – кругами.