Интерполяция методом Лагранжа
В общем случае, когда абсолютно ничего не известно об интерполируемой функции, сделать оценку для погрешности интерполяции невозможно Но такую оценку можно выполнить, если известны оценки для производных интерполируемой функции.
Внимание!
Погрешность при решении задачи интерполяции может быть вызвана следующими причинами. Во-первых, существует погрешность, связанная с неточностью заданных узловых точек и значений интерполируемой функции в этих точках Во-вторых, погрешность возникает при вычислениях из-за округления чисел с плавающей точкой. Наконец, существует погрешность вследствие замены исходной интерполируемой функции интерполяционным полиномом Здесь и далее речь идет именно о такой погрешности.
Предположим, что число узловых точек, по которым выполняется интерполяция, равно п+1. Это автоматически означает, что порядок интерполяционного полинома равен п.
На заметку
Если число интерполяционных точек равно n+1, то полином может иметь порядок и ниже п Это имеет место, например, в тех случаях, когда интерполируемая функция сама является полиномом степени, меньшей n.
Далее предположим, что производная порядка (n+1) от интерполируемой функции на интервале интерполирования не превышает по абсолютной величине значения М. Тогда погрешность интерполирования в точке х не превышает величины. Не затрагивая вопроса о том, как выполнить оценку для производной интерполируемой функции (это зависит от конкретных рассматриваемых ситуаций и выходит за рамки темологии книги), разработаем процедуру, которая будет автоматически определять погрешность интерполирования при заданном значении М.
Соответствующий программный код приведен ниже.
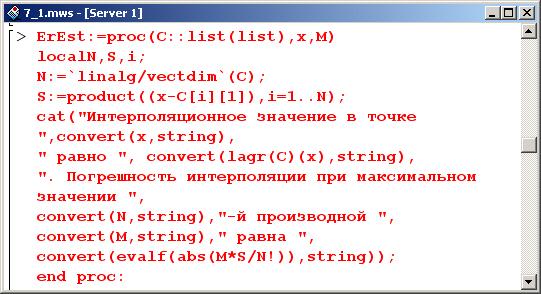
Процедура ErEst() имеет три параметра. Первым параметром является базовый список с интерполяционными точками. Второй и третий параметры – переменная интерполирования и оценка для производной интерполируемой функции соответственно.
Первой командой в теле процедуры определяется количество элементов в списке С. Для этого вызывается процедура vectdim() из пакета linalg. Полученное в результате число присваивается в качестве значения переменной N. Далее переменной S присваивается произведение, которое формируется процедурой product(). Множители в произведении– это разность переменной интерполирования и значения узловой точки. Ссылки на узловые точки выполнены в виде C[i][1] через индексную переменную!, которая пробегает значения от 1 до N. Погрешность интерполяции, таким образом, не превышает модуль (процедура abs()) величины MS/N1.
Внимание!
Элементы списка С нумеруются, начиная с индекса 1 и заканчивая индексом N. Число интерполяционных точек, таким образом, равно N. Порядок интерполяционного полинома равен N-1. Поэтому оценка М является верхней границей на интервале интерполирования для производной порядка N. Ведь порядок производной должен совпадать с числом точек и быть на единицу больше, чем порядок интерполяционного полинома. Отсюда в выражении для погрешности и далее для порядка производной указано N, а не N+1.
Результат выполнения процедуры оформляется в виде строки. Строка создается процедурой объединения cat(). Параметрами процедуры указаны базовые текстовые фразы вперемежку с командами преобразования численных выражений в строки. В последнем случае использована процедура convert () с опцией string.
Совет
Проверим, как работает созданная процедура. Для этого вызовем ее, указав в качестве базового интерполяционного списка созданный ранее генератором случайных чисел список В. Оценку для производной оставим в символьном виде. Кроме того, допускается использовать символьное выражение и для второго аргумента. Ниже приведен результат для точки х=2.5.
