Иллюстрированный самоучитель по Mathematica 3/4

Построение полиэдров (Polyhedra)

Для построения усеченных полиэдров предназначены следующие функции:

• Show [Truncate [Polyhedron [polyname] ] ] – построение усеченных полиэдров;
• Show [Truncate [Polyhedron [polyname], ratio] – построение усеченных полиэдров с заданным коэффициентом усечения ratio (от 0 до 0.5);
• Show[OpenTruncate[Polyhedron[polyname]]] – построение полиэдров с открытым усечением;
• Show[OpenTruncate[Polyhedron[polyname], ratio] – построение полиэдров с открытым усечением и заданным коэффициентом усечения ratio (от 0 до 0.5).

Рисунок 14.78 показывает построение усеченного полиэдра Усечение сделано так, будто полиэдр заполнен материалом. Поэтому усеченные области выглядят как дополнительные грани. Параметр ratio, задающий степень усечения, может иметь значения от 0 до 0.5 (в ином случае выводятся сообщения об ошибке в задании параметра).

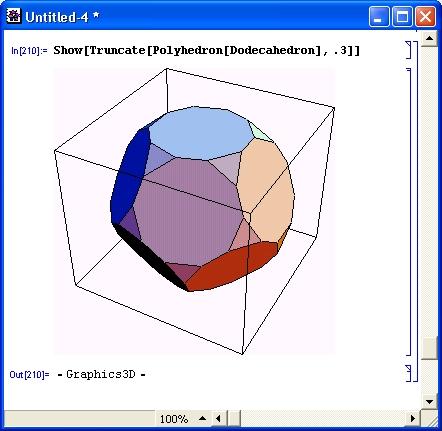
Рис. 14.78. Построение усеченного полиэдра

Усечение может быть открытым – такой вариант реализуется функцией со словом Open в имени. В этом случае фигура выглядит так, будто она склеена из тонкого картона (рис. 14.79). При этом в местах усечения фигура прозрачна.

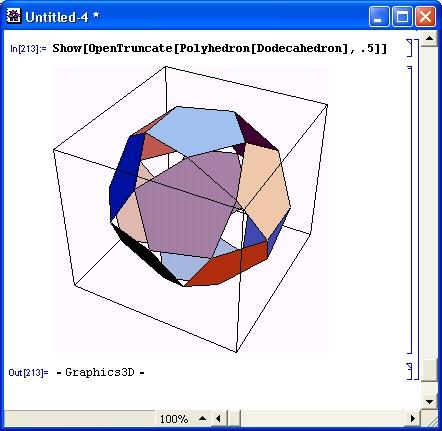
Рис. 14.79. Построение усеченного полиэдра с открытыми местами усечения

В заключение этого раздела отметим следующие функции:

• First [Polyhedron [polyname] ] – возвращает список полигонов для указанного полиэдра;
• Vertices [polyname] – возвращает список координат вершин полиэдра;
• Faces [polyname] – возвращает список вершин, ассоциированных с каждой гранью.

Они ничего не строят, а лишь возвращают специфические параметры полиэдров. Примеры применения этих функций представлены ниже:

Приведенные выше функции можно использовать на занятиях по стереометрии, где полученные с их помощью фигуры могут прекрасно иллюстрировать теоретические положения курса.