Создание поверхностей вращения (SurfaceOfRevolution)
Одна из задач компьютерной графики – создание поверхностей вращения. Средства для этого дает подпакет SurfaceOfRevolution. Они представлены следующими функциями:
- SurfaceOfRevolution [f, {x, xmin, xmax} ] – строит поверхность, образованную вращением кривой, описанной функцией f, при изменении х от xmin до xmax, в плоскости ху;
- SurfaceOfRevolution [{fx, f у}, {t, tmin, tmax} ] – строит поверхность, образованную вращением кривой, описываемой параметрически заданной на плоскости функцией {f x, f у}, в плоскости xz при изменении параметра t от tmin до tmax;
- SurfaceOfRevolution[{fx,fy,fz},{t,tmin,tmax}] – строит поверхность, образованную вращением кривой, описываемой параметрически заданной в пространстве функцией {fx, fy, fz}, в плоскости xz при изменении параметра t от tmin до tmax;
- SurfaceOfRevolution[f,{{x,xmin,xmax},{theta,thetamin,thetamax}}] – строит поверхность вращения кривой, описываемой функцией f, при угле theta, меняющимся от thetamin до thetamax.
Рисунок 14.88 дает простой пример построения поверхности, образованной линией cos(x) при изменении х от 0 до 4π, вращающейся вокруг оси xz. Построение задано функцией SurfaceOfRevolution [f, {x, xmin, xmax} ]. В этом случае линия вращается в пределах угла от 0 до 2π, поэтому поверхность получается круговой.
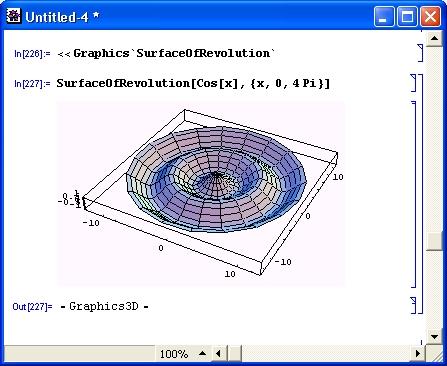
Рис. 14.88. Фигура, образованная вращением линии cos(x)
Следующий пример показывает ту же фигуру (рис. 14.89) в другом положении. Это достигается сменой угла обзора с помощью опции viewVertical.
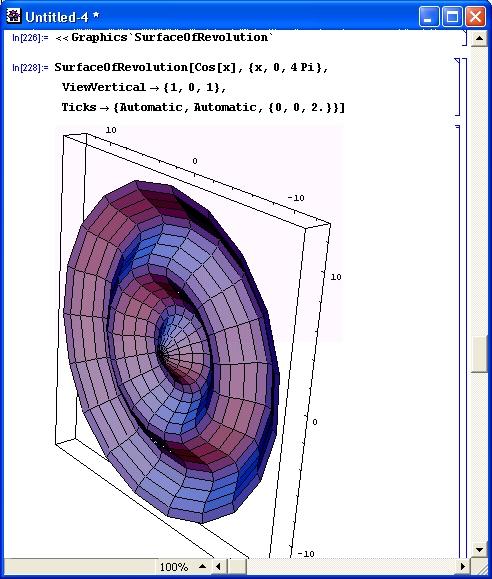
Рис. 14.89. Фигура рис. 14.88 в другом положении
