Примитивы, использующие сплайны (Spline)
Подпакет Spline вместе с уже описанным подпакетом NumericalMath'SplineFit' (сплайновая регрессия) обеспечивает представление данных с помощью сплайна. В подпакете Spline определена единственная функция Spline [points, type], которая создает графический примитив, представляющий сплайн-кривую типа type (Cubic, Bezier или CompoziteBezier – см. описание подпакета NumericalMath'SplineFit').
Среди ее опций важно отметить следующие (как и ранее, приведены значения, используемые по умолчанию): SplineDots › None, SplinePoints › 25, Max-Bend › 10.0 и SplineDivision › 20.0.
Рисунок 14.85 показывает задание массива из пяти точек на плоскости и соединение их отрезками прямых и кубическими сплайн-функциями. Хорошо видна аналогия сплайна с гибкой линейкой.
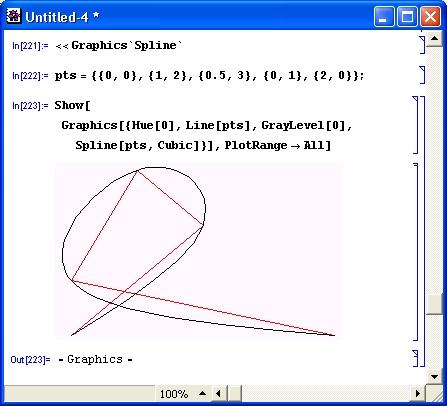
Рис. 14.85. Пример интерполяции пяти точек отрезками прямой и сплайнами
Сплайн-функции в данном случае применяются в порядке задания точек в списке pts. В этом случае возможно создание замкнутых линий (рис. 14.85 является наглядным примером этого).
Следует отметить, что хотя сплайн-аппроксимация дает хорошие результаты при умеренном числе точек, при малом их числе и неудачном выборе типа сплайнов результат может оказаться неудовлетворительным. Рисунок 14.86 иллюстрирует такую ситуацию.
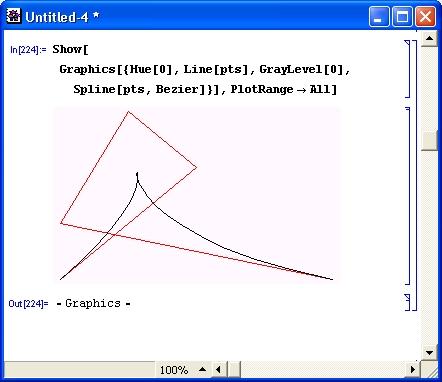
Рис. 14.86. Пример срыва сплайн-интерполяции точек
Рисунок 14.87 показывает возможность построения сплайн-функции вместе с точками, через которые она проходит.
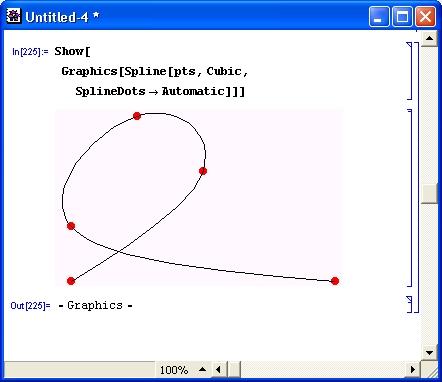
Рис. 14.87. Построение исходных точек и проходящей через них сплайн-функции
