Пакет числовой аппроксимации numapprox
Важным достоинством Паде-аппроксимации является возможность довольно точного приближения разрывных функций. Это связано с тем, что нули знаменателя у аппроксимирующего выражения способны приближать разрывы функций, если на заданном интервале аппроксимации число разрывов конечно.
На рис. 14.5 представлен пример Паде-аппроксимации функции tan(x) в интервале от -4.5 до 4.5, включающем два разрыва функции.
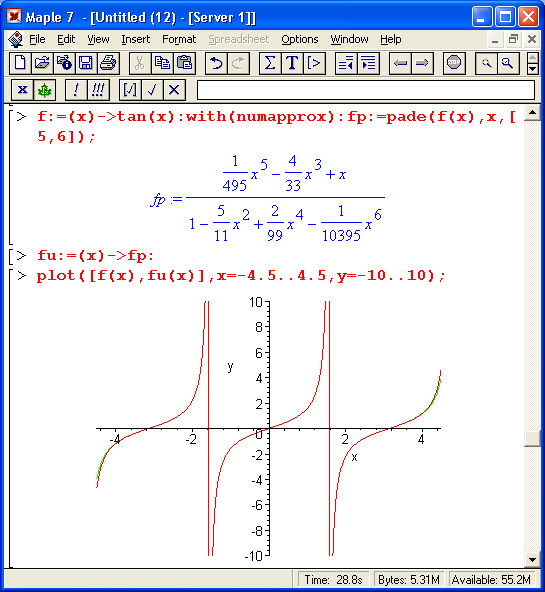
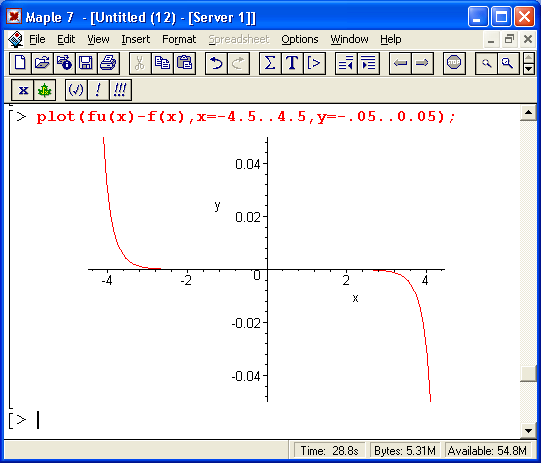
Рис. 14.5. Аппроксимация Паде для разрывной функции тангенса
Как видно из рис. 14.5, расхождение между функцией тангенса и ее аппроксимирующей функцией едва заметно лишь на краях интервала аппроксимации. Оба разрыва прекрасно приближаются аппроксимирующей функцией. Такой характер аппроксимации подтверждается и графиком погрешности, которая лишь на концах интервала аппроксимации [-4.0, 4.0] достигает значений 0.01 (около 1%).
