Пакет числовой аппроксимации numapprox
Паде-аппроксимация с полиномами Чебышева
Для многих аналитических зависимостей хорошие результаты дает аппроксимация полиномами Чебышева. В общем случае применяется Паде-аппроксимация отношением таких полиномов. Она реализуется функциями chebpade:
chebpade(f, x=a..b, [m.n]) chebpade(f., x, [m.n]) chebpade(f, a..b, [m,n])
Здесь а..b задает отрезок аппроксимации, m и n – максимальные степени числителя и знаменателя полиномов Чебышева.
Приведенный ниже пример показывает аппроксимацию Паде полиномами Чебышева для функции f=cos(x):
Наилучшая минимаксная аппроксимация
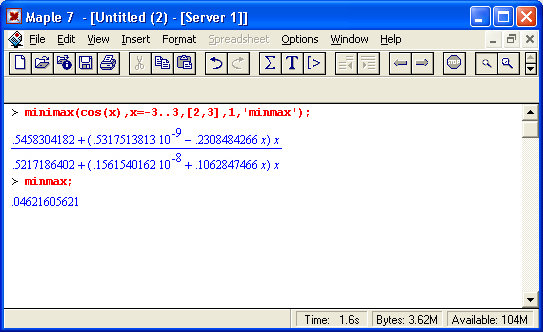
Минимаксная аппроксимация отличается от Паде-аппроксимации минимизацией максимальной абсолютной погрешности во всем интервале аппроксимации. Она использует алгоритм Ремеза (см. ниже) и реализуется следующей функцией:
mimmax(f, x=a..b, [m.n], w, 'maxerror') minimax(f, a..b, [m,n], w, 'maxerror')
Здесь помимо уже отмеченных параметров w – процедура или выражение, maxerror – переменная, которой приписывается значение minimax-нормы.
Ниже дан пример аппроксимации функции cos(x) в интервале [-3, 3]: