Пакет числовой аппроксимации numapprox
Наилучшая минимаксная аппроксимация по алгоритму Ремеза
Для получения наилучшей полиномиальной аппроксимации используется алгоритм Ремеза, который реализует следующая функция:
remez(w, f, a, b, m, n,_crit, 'maxerror')
Здесь w – процедура, представляющая функцию w(x) > 0 в интервале [a, b], f – процедура, представляющая аппроксимируемую функцию а и b – числа, задающие интервал аппроксимации [a,b], m и n – степени числителя и знаменателя аппроксимирующей функции, crit – массив, индексированный от 1 до m + n + 2 и представляющий набор оценок в критических точках (то есть точек максимума/минимума кривых погрешности), mахеrrоr – имя переменной, которой присваивается минимаксная норма wabs(f -r).
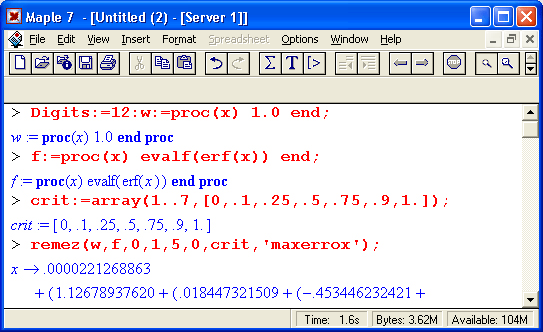
Следующий пример иллюстрирует применение данной функции для аппроксимации функции erf(x):
Другие функции пакета
Отметим назначение других функций пакета numapprox:
- chebdeg(p) – возвращает степень полинома Чебышева р;
- chebmult(p, q) – умножение полиномов Чебышева р и q;
- chebsort(e) – сортирует элементы ряда Чебышева;
- confracform(r) – преобразует рациональное выражение г в цепную дробь;
- confracform(r, х) – преобразует рациональное выражение г в цепную дробь с независимой переменной х;
- hornerform(r) – преобразует рациональное выражение г в форму Горнера;
- hornerform(r, х) – преобразует рациональное выражение г в форму Горнера с независимой переменной х;
- infnorm(f, x=a…b, 'xmax') – возвращает L-бесконечную норму функции на отрезке х [а, b];
- infnorm(f, a…b, 'xmax') – возвращает L-бесконечную норму функции на отрезке [а, b].
Действие этих функций очевидно, и читатель может самостоятельно опробовать их в работе.
