Пакет интегральных преобразований inttrans
Прямое и обратное преобразования Фурье
Прямое преобразование Фурье преобразует функцию времени f(t) в функцию частот и заключается в вычислении следующей интегральной функции:
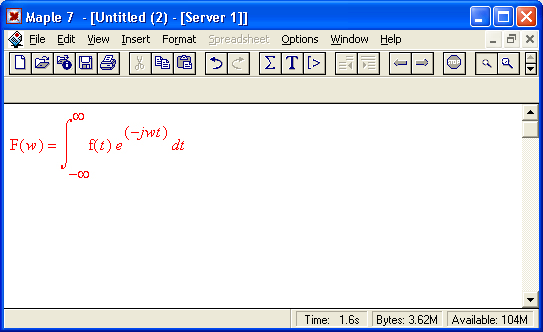
Оно реализуется следующей функцией пакета интегральных преобразований inttrans:
fourier(expr,t,w)
Здесь ехрr – выражение (уравнение или множество), t – переменная, от которой зависит ехрr, и w – переменная, относительно которой записывается результирующая функция.
Обратное преобразование Фурье задается вычислением интеграла:
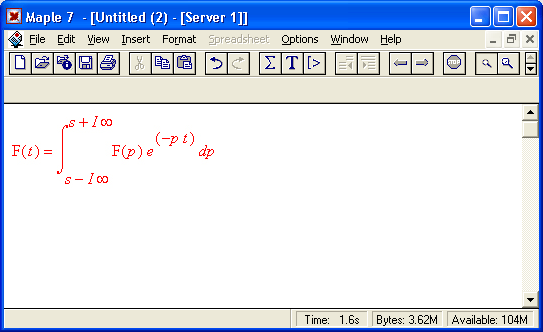
Оно фактически переводит представление сигнала из частотной области во временную.
Примеры применения преобразования Фурье представлены ниже:
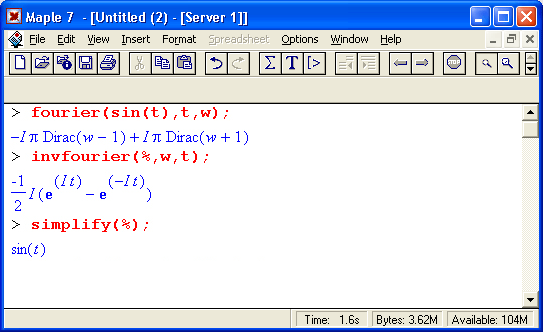
Обратите внимание на то, что даже в простом первом примере применение обратного преобразования Фурье вслед за прямым не привело к буквальному восстановлению исходной функции sin(t). Потребовалась команда simplify, чтобы перевести результат в виде представления синуса через экспоненциальные функции к обычному виду sin(t).
