Преобразования Фурье. Функции одномерного и многомерного прямого преобразования Фурье.
Теперь построим график спектральной плотности полученного сигнала с помощью прямого преобразования Фурье, по существу переводящего временное представление сигнала в частотное. Этот график в области частот до 300 Гц (см. рис. 17.6) строится с помощью следующих команд:
>> Y=fft(y,1024): >> Pyy=Y.*conj(Y)/1024; >> f=2000*(0:150)/1024; >> plot(f,Pyy(l:151)),gridГрафик спектральной плотности сигнала, построенный в этом примере, представлен на рис. 17.7. Даже беглого взгляда на рисунок достаточно, чтобы убедиться в том, что спектрограмма сигнала имеет явный пик на средней частоте амплитудно-модулированного сигнала и два боковых пика. Все эти три частотные составляющие сигнала явно выделяются на общем шумовом фоне. Таким образом, данный пример наглядно иллюстрирует технику обнаружения слабых сигналов на фоне шумов, лежащую в основе работы радиоприемных устройств.
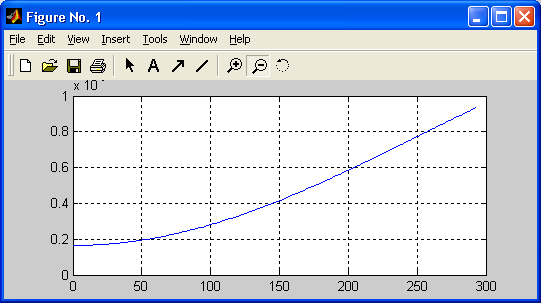
Рис. 17.7. График спектральной плотности приведенного на рис. 17.6 сигнала
Функции многомерного прямого преобразования Фурье
Для двумерного прямого преобразования Фурье используется функция fft2:
- fft2(X) – возвращает для массива данных X двумерное дискретное преобразование Фурье;
- fft2(X,m.n) – усекает массив X или дополняет его нулями, чтобы перед выполнением преобразования Фурье создать матрицу размера тхп. Результат – матрица того же размера.
Для многомерного прямого преобразования Фурье также существует функция:
- fftn(X) – возвращает результат N-мерного дискретного преобразования для массива X размерности N. Если X – вектор, то выход будет иметь ту же ориентацию;
- fftn(X.siz) – возвращает результат дискретного преобразования для массива X с ограничением размера, заданным переменной siz.
