Иллюстрированный самоучитель по MatLab

Интерполяция и аппроксимация данных. Полиномиальная регрессия.

Под аппроксимацией обычно подразумевается описание некоторой, порой не заданной явно, зависимости или совокупности представляющих ее данных с помощью другой, обычно более простой или более единообразной зависимости. Часто данные находятся в виде отдельных узловых точек, координаты которых задаются таблицей данных.

Результат аппроксимации может не проходить через узловые точки. Напротив, задача интерполяции – найти данные в окрестности узловых точек. Для этого используются подходящие функции, значения которых в узловых точках совпадают с координатами этих точек. Например, при линейной интерполяции зависимости у(х) узловые точки соединяются друг с другом отрезками прямых и считается, что искомые промежуточные точки расположены на этих отрезках.

Для повышения точности интерполяции применяют параболы (квадратичная интерполяция) или полиномы более высокой степени (полиномиальная интерполяция). Для обработки данных MATLAB использует различные функции интерполяции и аппроксимации данных. Набор таких функций вместе с несколькими вспомогательными функциями описан в этом разделе.

Одна из наиболее известных аппроксимаций – полиномиальная. В системе MATLAB определены функции аппроксимации данных полиномами по методу наименьших квадратов – полиномиальной регрессии. Это выполняет функция, приведенная ниже:

• polyfit(x.y.n) – возвращает вектор коэффициентов полинома р(х) степени п, который с наименьшей среднеквадратичной погрешностью аппроксимирует функцию у(х). Результатом является вектор-строка длиной n+1, содержащий коэффициенты полинома в порядке уменьшения степеней х и у равно n+1, то реализуется обычная полиномиальная аппроксимация, при которой график полинома точно проходит через узловые точки с координатами (х.у), хранящиеся в векторах х и у. В противном случае точного совпадения графика с узловыми точками не наблюдается;
• [p.S] = polyflt(x.y.n) – возвращает коэффициенты полинома р и структуру S для использования вместе с функцией polyval с целью оценивания или предсказания погрешности;
• [p.S] = polyfit(x,y,n,mu) возвращает коэффициенты полинома р и структуру S для использования вместе с функцией polyval с целью оценивания или предска-зния погрешности, но так, что происходит центрирование (нормирование) и масштабирование х, xnorm = (х -mu(l))/mu(2), где mu(l) = mean(x) и mu(2) = std(x). Центрирование и масштабирование не только улучшают свойства степенного многочлена, получаемого при помощи polyval, но и значительно повышают качественные характеристики самого алгоритма аппроксимации.

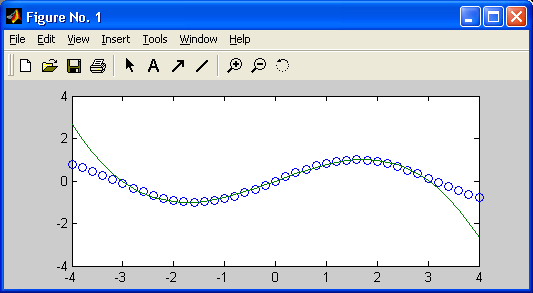
Рис. 17.10. Пример использования функции polyfit

Пример (полиномиальная регрессия для функции s:

Рисунок 17.14, построенный в этом примере, дает наглядное представление о точности полиномиальной аппроксимации. Следует помнить, что она достаточно точна в небольших окрестностях от точки х = 0, но может иметь большие погрешности за их пределами или в промежутках между узловыми точками.

График аппроксимирующего полинома третьей степени на рис. 17.10 показан сплошной линией, а точки исходной зависимости обозначены кружками. К сожалению, при степени полинома свыше 5 погрешность полиномиальной регрессии (и аппроксимации) сильно возрастает и ее применение без центрирования и масштабирования становится рискованным. Обратите внимание на то, что при полиномиальной регрессии узловые точки не ложатся точно на график полинома, поскольку их приближение к нему является наилучшим в смысле минимального среднеквадратического отклонения. Об этом уже говорилось.