Преобразования Фурье. Функции одномерного и многомерного прямого преобразования Фурье.
Разработка преобразований Фурье сыграла огромную роль в появлении и развитии ряда новых областей науки и техники. Достаточно отметить, что электротехника переменного тока, электрическая связь и радиосвязь базируются на спектральном представлении сигналов. Ряды Фурье также можно рассматривать как приближение произвольных функций (определенные ограничения в этом известны) тригонометрическими рядами бесконечной длины. При конечной длине рядов получаются наилучшие среднеквадратические приближения. MATLAB содержит функции для выполнения быстрого одномерного и двумерного быстрого дискретного преобразования Фурье. Для одномерного массива*с длиной N прямое и обратное преобразования Фурье реализуются по следующим формулам:
Прямое преобразование Фурье переводит описание сигнала (функции времени) из временной области в частотную, а обратное преобразование Фурье переводит описание сигнала из частотной области во временную. На этом основаны многочисленные методы фильтрации сигналов.
В описанных ниже функциях реализован особый метод быстрого преобразования Фурье – Fast Fourier Transform (FFT, или БПФ), позволяющий резко уменьшить число арифметических операций в ходе приведенных выше преобразований. Он особенно эффективен, если число обрабатываемых элементов (отсчетов) составляет 2т, где т – целое положительное число. Используется следующая функция:
- fft(X) – возвращает для вектора X дискретное преобразование Фурье, по возможности используя алгоритм быстрого преобразования Фурье. Если X – матрица, функция fft возвращает преобразование Фурье для каждого столбца матрицы;
- fft(X.n) – возвращает n-точечное преобразование Фурье. Если длина вектора X меньше n, то недостающие элементы заполняются нулями. Если длина X больше п, то лишние элементы удаляются. Когда X – матрица, длина столбцов корректируется аналогично;
- fft(X,[ Ldirn) и fft(X,n,dim) – применяют преобразование Фурье к одной из размерностей массива в зависимости от значения параметра dim.
Для иллюстрации применения преобразования Фурье создадим трехчастотный сигнал на фоне сильного шума, создаваемого генератором случайных чисел:
>> t=0:0.0005:1; >> x=sin(2*pi*200*t)+0.4*sin(2*pi*150*t)+0.4*sin(2*pi*250*t); >> y=x+2*randn(size(t)); >> plot(y(1:100),'b')
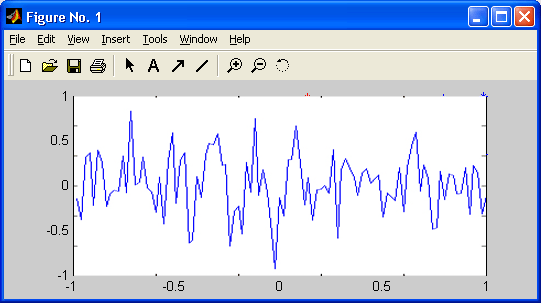
Рис. 17.6. Форма зашумленного сигнала
Этот сигнал имеет среднюю частоту 200 рад/с и два боковых сигнала с частотами 150 и 250 рад/с, что соответствует амплитудно-модулированному сигналу с частотой модуляции 50 рад/с и глубиной модуляции 0.8 (амплитуда боковых частот составляет 0.4 от амплитуды центрального сигнала). На рис. 17.6 показан график этого сигнала (по первым 100 отсчетам из 2000). Нетрудно заметить, что из него никоим образом не видно, что полезный сигнал – амплитудно-модулированное колебание, настолько оно забито шумами.
