Оценка погрешности аппроксимации. Сплайновая интерполяция в графическом окне.
Средства обработки данных из графического окна позволяют строить столбцовый или линейчатый график погрешностей в узловых точках и наносить на эти графики норму погрешности. Норма дает статистическую оценку среднеквадратической погрешности. Чем она меньше, тем точнее аппроксимация. Для вывода графика погрешности надо установить птичку у параметра Plot residuals (График погрешностей) и в меню ниже этого параметра выбрать тип графика.
Таким образом, интерфейс графического окна позволяет выполнять эффективную обработку данных наиболее распространенными способами.
Сплайновая интерполяция в графическом окне
Попытка аппроксимации полиномом 8-й степени не дает положительного результата – кривая проходит внутри облака точек, совершенно не интерполируя это облако.
Однако если применить сплайновую интерполяцию, то картина кардинально меняется. На этот раз кусочная линия интерполяции прекрасно проходит через все точки и поразительно напоминает синусоиду. Даже ее пики со значениями 1 и -1 воспроизводятся удивительно точно, причем и в случаях, когда на них не попадают узловые точки.
Причина столь великолепного результата кроется в уже отмеченных ранее особенностях сплайновой интерполяции – она выполняется по трем ближайшим точкам, причем эти тройки точек постепенно перемещаются от начала точечного графика функции к ее концу. Кроме того, непрерывность первой и второй производных при сплайновой интерполяции делает кривую очень плавной, что характерно и для первичной функции – синусоиды. Так что данный пример просто является удачным случаем применения сплайновой интерполяции.
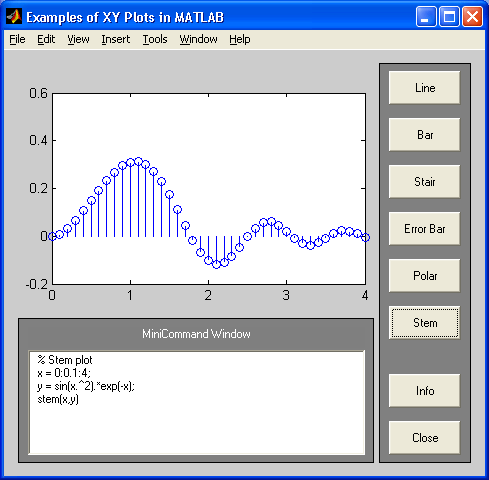
Рис. 17.15. Пример сплайновой интерполяции в графическом окне
Мы не можем практически называть этот подход полноценной аппроксимацией, поскольку в данном случае нет единого выражения для аппроксимирующей функции. На каждом отрезке приближения используется кубический полином с новыми коэффициентами. Поэтому и вывода аппроксимирующей функции в поле графика не предусмотрено.
