Интерполяция на неравномерной сетке
Для интерполяции на неравномерной сетке используется функция griddata:
- ZI = griddata(x.y.z.XI.YI) – преобразует поверхность вида z = f(x. у), которая определяется векторами (x.y.z) с (обычно) неравномерно распределенными элементами. Функция griddata аппроксимирует эту поверхность в точках, определенных векторами (XI.YI) в виде значений ZI. Поверхность всегда проходит через заданные точки. XI и YI обычно формируют однородную сетку (созданную с помощью функции meshgrid).
XI может быть вектором-строкой, в этом случае он определяет матрицу с постоянными столбцами. Точно так же YI может быть вектором-столбцом, тогда он определяет матрицу с постоянными строками.
- [XI.YI.ZI] = griddata(x,y,z,xi,yi) – возвращает аппроксимирующую матрицу ZI, как описано выше, а также возвращает матрицы XI и YI, сформированные из вектора-столбца xi и вектора-строки yi. Последние аналогичны матрицам, возвращаемым функцией meshgrid;
- […] = griddata (….method) – использует определенный метод интерполяции:
- 'nearest' – ступенчатая интерполяция;
- 'linear' – линейная интерполяция (принята по умолчанию);
- 'cubic' – кубическая интерполяция;
- ' v4 ' – метод, используемый в МATLAB 4.
Метод определяет тип аппроксимирующей поверхности. Метод 'cubic' формирует гладкие поверхности, в то время как 'linear' и 'nearest' имеют разрывы первых и нулевых производных соответственно. Все методы, за исключением v4, основаны на триангуляции Делоне. Метод ' v4 ' включен для обеспечения совместимости с версией 4 системы MATLAB. Пример:
>> x=rand(120.1)*4-2;y=rand(120.1)*4-2; z=x,*y,*exp(-x.^2-y.^2); >> t=-2:0.1:2;[X,Y]=meshgrid(t,t); Z=griddata(x.y.z.X.Y); >> mesh(X.Y.Z),hold on;plot3(x.y,z, 'ok')Функции griddataS и griddatan работают аналогично griddata, но для для трехмерного и n-мерного случая – с использованием алгоритма qhul 1. Используются, в частности, при трехмерной и n-мерной триангуляции.
Рисунок 17.13 иллюстрирует применение функции griddata.
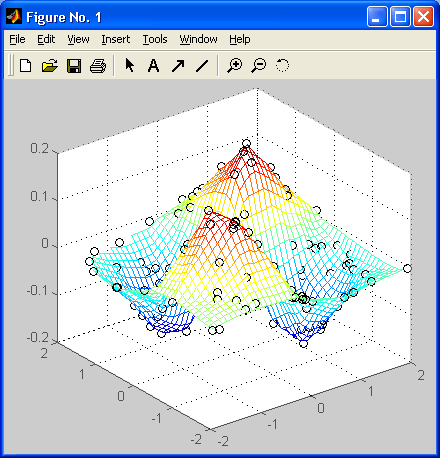
Рис. 17.12. Пример использования функции griddata
