Вычисление площади полигона
В системе MATLAB определены функции, вычисляющие площадь полигона и анализирующие нахождение точек внутри полигона. Для вычисления площади полигона используется функция polyarea:
- polyarea(X.Y) – возвращает площадь полигона, заданного вершинами, находящимися в векторах X и Y. Если X и Y – матрицы одного размера, то polyarea возвращает площадь полигонов, определенных столбцами X и Y;
- polyarea(X.Y.dim) – возвращает площадь полигона, заданного столбцами или строками X и Y в зависимости от значения переменной dim. Пример:
>> L = linspace(0.3*pi,10); >> X= sin(L)'; >> Y=cos(L)'; >> A = polyarea(X.Y) A =3.8971>> plot(X.Y.'m')
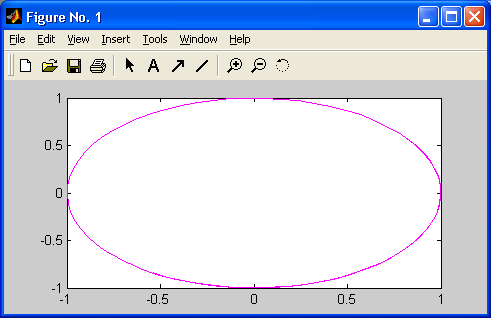
Рис. 17.3. Область многоугольника, для которого вычислена площадь
Построенный по этому примеру многоугольник представлен на рис. 17.3. В данном примере использована функция linspace(x1.x2,N), генерирующая N точек в промежутке от x1 до х2 с последующим формированием векторов X и Y для построения многоугольника в полярной системе координат.
