Иллюстрированный самоучитель по MatLab

Двумерная табличная интерполяция

Двумерная интерполяция существенно сложнее, чем одномерная, рассмотренная выше, хотя смысл ее тот же – найти промежуточные точки некоторой зависимости z(x, у) вблизи расположенных в пространстве узловых точек. Для двумерной табличной интерполяции используется функция interp2:

• ZI = interp2(X,Y.Z,XI.YI) – возвращает матрицу ZI, содержащую значения функции в точках, заданных аргументами XI и YI, полученные путем интерполяции двумерной зависимости, заданной матрицами X, Y и Z. При этом X и Y должны быть монотонными и иметь тот же формат, как если бы они были получены с помощью функции meshgrid (строки матрицы X являются идентичными; то же можно сказать о столбцах массива Y). Матрицы X и Y определяют точки, в которых задано значение Z. Параметры XI и YI могут быть матрицами, в этом случае interp2 возвращает значения Z, соответствующие точкам (XI(i,j),YI(i.j)). В качестве альтернативы можно передать в качестве параметров вектор-строку xi и вектор-столбец yi. В этом случае interp2 представляет эти векторы так, как если бы использовалась команда mesh-grid(xi.yi);
• ZI = interp2(Z,XJ.YI) – подразумевает, что Х=1:n и Y=l:m, где [m.n]=size(Z);
• ZI = interp2(Z,ntimes) – осуществляет интерполяцию рекурсивным методом с числом шагов ntimes;
• ZI = interp2(X,Y,Z.XI,YI.method) – позволяет с помощью опции method задать метод интерполяции:
  • 'nearest' – интерполяция по соседним точкам;
  • 'linear' – линейная интерполяция;
  • 'cubic' – кубическая интерполяция (полиномами Эрмита);
  • 'spline' – интерполяция сплайнами.

Все методы интерполяции требуют, чтобы X и Y изменялись монотонно и имели такой же формат, как если бы они были получены с помощью функции meshgrid. Когда X и Y – векторы равномерно распределенных точек, для более быстрой интерполяции лучше использовать методы '*1inear', '*cubic', или '*nearest'.

Пример:

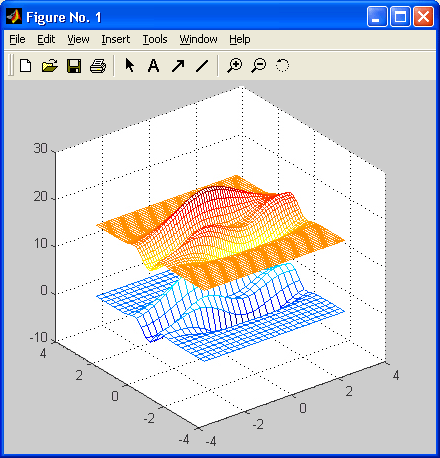
Рис. 17.13. Применение функции interpZ

Рисунок 17.13 иллюстрирует применение функции interp2 для двумерной интерполяции (на примере функции peaks).

В данном случае поверхность снизу – двумерная линейная интерполяция, которая реализуется по умолчанию, когда не указан параметр method.