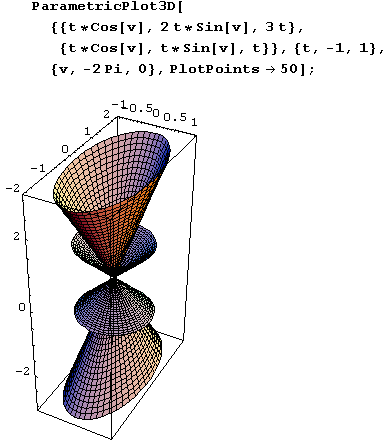Вычерчивание графиков
Построение параметрически заданных кривых и поверхностей – функция ParametricPlot3D
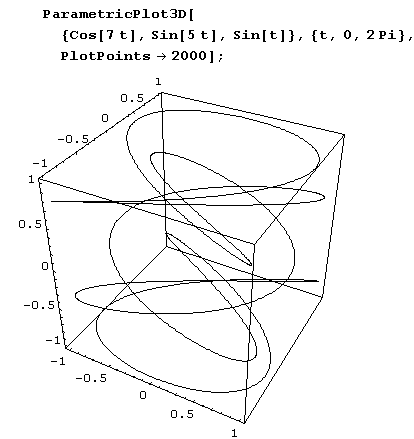
Далеко не все поверхности можно задать уравнением z = f(x,y)) или таблично. Часто гораздо удобнее задавать их параметрически. Параметрически можно задать также кривые в пространстве. Параметрически заданные в трехмерном пространстве двухмерные поверхности или одномерные кривые можно рисовать с помощью функции ParametricPlot3D. Проекцией нарисованной ниже кривой является фигура Лиссажу.
Вызов ParametricPlot3D[ {xt, yt, it], {t, tmin, tmax}] возвращает пространственную кривую, параметризованную переменной /, изменяющейся от tmin до tmах.
Вызов же ParametricPlot3D[ {xt, yt, zt}, {t, tmin, tmax}, {u, umin, umax}] возвращает поверхность в пространстве, параметризованную переменными t и и, изменяющимися от tmin до tmax и от umin до umах соответственно. Можно указать оттенок рисуемого образа, для этого вызов нужно записать так: ParametricPlotSD [{xt, yt, zt, оттенок},…].
Ну и, конечно, можно нарисовать несколько образов. Для этого вызов записывается так: ParametricPlotSD [{(xlt, ylt, zJt}, (x2t, y2t, z2t),…},…]. На рисунке ниже хорошо видно, что кривые x=tcost, y=tsint, z= 2t и х= 2 t cos t, у = 2t sin t, z = 2 t лежат на конусах.
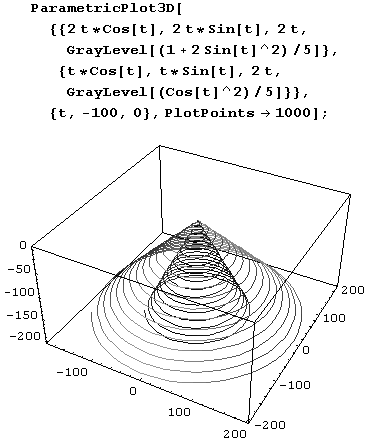
Для оттенения этих конических винтовых линий (создания эффекта их освещения) применялась функция GrayLevel. Это "освещение" несколько необычно: там, где одна коническая винтовая линия темнеет, вторая светлеет.
На следующем рисунке показаны конусы с общей вершиной.