Несколько графиков на одном чертеже (функция GraphicsArray)
Как вы уже знаете, функция GraphicsArray позволяет на одном листе (чертеже) нарисовать несколько графиков, расположив их в одну строку или в виде двухмерного массива. Однако если вы все графики вычерчиваете с помощью одной функции, например ParametricPlot, удобно предварительно установить те значения ее опций, которые совпадают у большинства графиков.
Пусть, например, мы хотим установить опции AspectRatio › Automatic и Axes › False.
Вот как это делается:
SetOptions[ParametricPlot,AspectRatio > Automatic,Axes > False];Теперь можем определить нужные нам графики и при необходимости задать значения тех опций, которые отличаются от установленных ранее. Пусть, например, на первом и третьем графиках вычерчиваются оси координат. Тогда для этих графиков устанавливаем Axes › True.
Block[{$DisplayFunction=Identity}, p1=ParametricPlot[{Cos[t],Sinft]},{t,0.2Pi},Axes > True]; p2=ParametricPlot[{2*Cos[t],Sin[t]),{t,0.2Pi}]; p3=ParametricPlot[{ (2*Cos [t] - 1) Cos[t-], (2*Cos[t]-1) Sin[t] },{t,0.2Pi},Axes > True]; p4=ParametricPlot[{t Cos[t],t Sin[t]},{t,0.12Pi}]; p5=ParametricPlot[{t Cos[t]Sin[t],t Sin[t]^2},{t,0.8Pi}]; p6=ParametricPlot[{Sin[2t]+Sin[5t],Cos[2t]+Cos[5 t]},{t,0.2Pi}]; p7=ParametricPlot[{Sin[2t]Sin[5t],Cos[2t]Sin[5t]},{t,0.2Pi}]; p8=ParametricPlot[{Cos[t]+1/2Cos[7t]+1/3 Cos[-17t+Pi/2],Sin[t]+1/2 Sin[7 t]+1/3*Sin[-17t+Pi/2]},{t,0.2Pi}];]После этого формируем массив графиков и отображаем его.
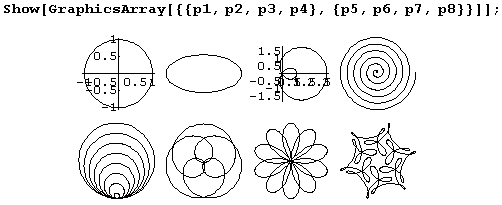
Функция GraphicsArray может быть полезна при подборе параметров.
Пример 9.18. Подбор параметров с помощью функции GraphicsArray.
Предположим, вам нужно среди двухпараметрического множества кривых (напоминающих цветы) вида (R cos(az), R sin(fe)), где R = sin 5r, выбрать ту, которая ближе всего к окружности при условии, что параметры а и b принимают целые значения, причем 1<а<9 и 1<6<6. Можно, конечно, пересмотреть все 54 кривые по одной. Но если вы не уверены, что среди них есть окружность, лучше расположить все графики на одном чертеже.
Однако в отличие от предыдущих примеров, где количество графиков было небольшим, в данном случае формирование массива лучше всего поручить системе Mathematica. Для этого как нельзя лучше приспособлена функция Table. Именно с ее помощью удобнее всего сначала сформировать двухмерный массив шириной 6 и высотой 9 графиков. Затем эти графики лучше всего отобразить на одном чертеже и выбрать (на глаз) те, которые, как вам кажется, наиболее подходят для вашей цели. Отобранные графики затем можно будет рассмотреть в деталях и выбрать наиболее подходящий из них. Вот как это делается в нашем случае.
Block[{k=5},Block[{a,b,r=Sin[k*z]}, Block[{XY={r*Cos[a*z],r*Sin[b*z]}), Show[GraphicsArray[ Table[Table[ParametricPlot[XY,{z,0.2 Pi}],{b,6}],{a,9}]]]]]]